Introduction
The ultimate guide to mastering the cs interview
基础篇
基础篇
与其他语言相比,使用 Go 有什么好处?
- 简洁和高效的语法
- 高效的并发处理(轻量级 Goroutine/内置并发原语)
- 内存管理
- 跨平台编译
- 适合云原生和微服务
for range
1.23
值传递和指针传递区别
数据类型
字符串
字符串在 Go 中是不可变类型。string本质是一个结构体底层是由 str 指针和 len 组成。
type stringStruct struct {
str unsafe.Pointer
len int
}
string 与 []byte 转换会发生内存拷贝?
- byte 是unit8 别名
- string本质是一个结构体底层是由 str 指针 和 len 组成。一个byte类型数组
- string 类型是不能更改。但stringStruct 中str 指针可以改变,指向的内容不可变。可以看出来,指针指向的位置发生了变化,也就是每更改一次字符串,就需要重新分配一次内存,之前分配的空间会被gc;
- 将string的底层数组从头部复制n个到[]byte对应的底层数组中去,预先定义一个长度为32的数组,字符串的长度超过了这个数组的长度,就重新分配一块内存,否则就是用预先分配的内存来做
- 标准方法发生内存拷贝,更安全
字符串拼接性能
- +操作符:
- 优点: 语法简单,直观易懂。
- 缺点: 在大量字符串拼接时,每次 + 操作都会创建新的字符串对象,会引发多次内存分配和复制,性能较差。 时间复杂度为 O(n^2),因为每次都要复制整个字符串。
str := "Hello, " + "world!" - strings.Join() 函数:
- 优点: 使用 strings.Join() 函数进行拼接,只需要遍历一次待拼接的字符串数组,内存分配和复制次数较少,性能较好。
- 缺点: 需要将字符串数组转换为切片,有一定的性能开销。
strs := []string{"Hello", "world", "!"} result := strings.Join(strs, " ")
时间复杂度为 O(n),其中 n 是所有字符串的总长度。
-
fmt.Sprintf() 函数:
- 优点: 支持格式化输出,可以方便地构建复杂的格式化字符串。 由于 fmt.Sprintf() 是一次性完成字符串拼接的,因此对于少量字符串拼接时性能较好。
- 缺点: 对于大量的字符串拼接,由于每次调用 fmt.Sprintf() 都会创建新的字符串对象,因此性能较差。 时间复杂度取决于字符串的总长度。
name := "John" age := 30 str := fmt.Sprintf("Name: %s, Age: %d", name, age) -
strings.Builder 类型:
- 优点: 在循环中进行字符串拼接时性能优于其他方法。 strings.Builder 类型内部使用了缓冲区,避免了频繁的内存分配和复制,因此性能较好。
- 缺点: 语法相对复杂,不如其他方法直观易懂。
var builder strings.Builder for i := 0; i < 10; i++ { builder.WriteString("Iteration ") builder.WriteString(strconv.Itoa(i)) builder.WriteString("\n") } result := builder.String()
综上所述,性能最优的字符串拼接方法取决于具体的场景和需求。对于大量字符串拼接的情况,strings.Builder 是性能最好的选择;对于少量且需要格式化的情况,fmt.Sprintf() 是一个不错的选择;而对于简单的拼接操作,strings.Join() 通常也能满足需求。尽管 + 操作符简单直观,但在大量拼接时会导致性能问题,应尽量避免在性能敏感的代码中使用。
数字类型
- int,uint
- int8,uint8
- int16,uint16
- int32,uint32
- int64,uint64
- float32
- float64
- complex64
- complex128
rune 类型
- rune int32 别名
- 一个 rune值代表一个 Unicode字符
uintptr
array 类型
- len() == cap()
- 数组是单一内存块,并无其他附加结构
- 初始化多维数组,仅第一维度允许用
... - 支持数字指针直接访问
- 直接获取元素指针
- 值传递,复制整个数组 指针
- 数组指针:
&array指向整个数组的指针 - 元素指针:
&array[0]指向某个元素指针 - 指针数组:
[...]*int{&a, &b}元素是指针的数组 复制 - 数组传递会复制整个数组,可用指针或切片代替
nil
- 两个nil 不能比较,nil 是无类型
- 声明一个nil 的Map,可读不可写
- 关闭nil的channel 会panic
- nil 切片不能索引访问
- 方法接受者是nil, 调用方法也会panic
- 空指针是一个灭有任何值的指针
slice 类型
struct 类型
function 类型
map 类型
channel 类型
interface 类型
make 和 new 的区别?
在Go语言中,new 和 make 是两个用于分配内存的内建函数,它们分别用于不同类型的数据结构,主要用途如下:
new 关键字
new 用于分配内存,但不初始化内存,返回的是指针。 主要用于创建值类型(如结构体、数组、基本类型等)的实例。 返回值: 返回的是指向类型零值的指针。 示例:
// 示例:创建一个指向 int 的指针
ptr := new(int)
*ptr = 10
make 函数
用途: make 用于创建切片、映射和通道等引用类型的数据结构。
在内部分配内存,并对其进行初始化,返回的是对应的引用类型(切片、映射、通道)。
返回值: 返回的是引用类型(切片、映射、通道)本身,而不是指针。
示例:
// 示例:创建一个切片
slice := make([]int, 5, 10)
总结
- new 可以用于任何类型的分配内存,而 make 仅限于切片、映射和通道等引用类型。
- 返回值: new 返回指向零值的指针,而 make 返回初始化后的引用类型本身。
- 初始化: new 不进行内部的初始化,而 make 在分配内存后会进行必要的初始化操作。
- 适用场景:
- 使用 new 时,你通常需要对零值进行修改或者设置,比如对结构体字段进行赋值。
- 使用 make 时,你通常会在切片、映射和通道等引用类型上进行操作,并且需要确保它们被正确地初始化。
切片
切片是一个动态数组的抽象,以指针引用底层数组,限定读写区域。
// runtime/slice.go
type slice struct {
array unsafe.Pointer
len int
cap int
}
- 引用类型,未初始化为
nil - 基于数组,初始化值或
make函数创建 len元素数量,cap返回容量- 不支持
==,!=操作
切片截取
截取时常见创建 slice 的方法,可以从数组或者 slice 中直接截取,需要制定起止索引位置。
值得注意的时,截取的新老 slice 相互影响的前提时共用底层数组,如果因为 append 操作使得
新 slice 底层数组扩容列,移动到新的位置,那么二者就不会相互影响了。
截取操作:data[low,high,max], max>=high>=low
例如:
old := []int{0,1,2,3,4,5,6,7,8,9}
new1 := old[2:5] // new1 从索引2闭区间到索引5开区间即真正索引4位置,长度为3,容量到数组末尾即8
// new1 == [2,3,4,x,x,x,x,x] // len=3 cap=8 x:表示空
new2 := new1[2:6:7] // 从new1中2-6截取,容量到索引7,即cap=7-2=5
// new2 == [4,5,6,7,x] 因为容量还是小于old 所以还是在底层数据操作
new2 = append(new2, 100) // new2 的 len == cap == 5 长度达到容量了
new2 = append(new2, 200) // new2 需要扩容了
new1[2] = 20 // 只会更改new1 和 old slice,new2 已经不与他们共用底层数组了
fmt.Println(old) // [0,1,2,3,20,5,6,7,100,9]
fmt.Println(new1) // [2,3,20]
fmt.Println(new2) // [4,5,6,7,100,200]
Go 语⾔是如何实现切⽚扩容的?
- Go1.18之前切片的扩容是以容量1024为临界点
- 当旧容量 < 1024个元素,扩容变成2倍;
- 当旧容量 > 1024个元素,那么会进入一个循环,每次增加25%直到大于期望容量。
- 然而这个扩容机制已经被Go 1.18弃用了,官方说新的扩容机制能更平滑地过渡。就是控制让小的切片容量增长速度快一点,减少内存分配次数,而让大切片容量增长率小一点,更好地节省内存。
- Go 1.17切片扩容时会进行内存对齐,这个和内存分配策略相关。进行内存对齐之后,新 slice 的容量是要 大于等于老 slice 容量的 2倍或者1.25倍。
- 当新切片需要的容量cap大于两倍扩容的容量,则直接按照新切片需要的容量扩容;
- 当原 slice 容量 < 1024 的时候,新 slice 容量变成原来的2倍;
- 当原 slice 容量 > 1024,进入一个循环,每次容量变成原来的1.25倍,直到大于期望容量。
- Go1.18不再以1024为临界点,而是设定了一个值为256的
threshold,以256为临界点;超过256,不再是每次扩容1/4,而是每次增加(旧容量+3*256)/4;- 当新切片需要的容量cap大于两倍扩容的容量,则直接按照新切片需要的容量扩容;
- 当原 slice 容量 < threshold 的时候,新 slice 容量变成原来的 2 倍;
- 当原 slice 容量 > threshold,进入一个循环,每次容量增加(旧容量+3*threshold)/4。
- 切片的扩容都是调用 growSlice 方法;
Go1.18 版本func growslice(et *_type, old slice, cap int) slice { // 新容量默认为原有容量 newcap := old.cap doublecap := newcap + newcap // 如果新容量大于旧容量的两倍,则直接按照新容量大小申请 if cap > doublecap { newcap = cap } else { // 如果原有长度小于1024,则新容量是旧容量的2倍 if old.len < 1024 { newcap = doublecap } else { // 按照原有容量的 1/4 增加,直到满足新容量的需要 for 0 < newcap && newcap < cap { newcap += newcap / 4 } // 检查容量是否溢出。 if newcap <= 0 { newcap = cap } } } }func growslice(et *_type, old slice, cap int) slice { ... newcap := old.cap doublecap := newcap + newcap if cap > doublecap { newcap = cap } else { const threshold = 256 if old.cap < threshold { newcap = doublecap } else { // Check 0 < newcap to detect overflow // and prevent an infinite loop. for 0 < newcap && newcap < cap { // Transition from growing 2x for small slices // to growing 1.25x for large slices. This formula // gives a smooth-ish transition between the two. newcap += (newcap + 3*threshold) / 4 } // Set newcap to the requested cap when // the newcap calculation overflowed. if newcap <= 0 { newcap = cap } } } ... } - 切片在扩容时会进行内存对齐,这个和内存分配策略有关,进行内存对齐后切片扩容的容量要大于等于旧的切片容量的2倍或者1.25倍,当原切片容量小于1024的时候,新切片容量按照原来的2倍进行扩容,原slice容量超过1024的时候,新slice容量变成原来的1.25倍。
总结:尽量对切片设置初始容量值,以避免 append 调用 growslice,因为新的切片容量比旧的大,会开辟新的地址,拷贝数据,降低性能。
Map
Map 是什么
map 是由一组 <key,value> 对组成的抽象数据结构,并且同一个 key 只会出现一次。 Go 的 map 底层是一个哈希表,包含若干 bucket(桶)。每个 bucket 是一个包含多个键值对的结构。
- map 相关的操作主要有:增删改查
- 数据结构:
- 哈希查找表 O(N)
- 哈希表存在碰撞问题,解决方法
- 链表法:将一个 bucket 实现成一个链表,落在同一个 bucket 的 key 都会插入这个链表
- 开放地址法:按照一定的规律,在 bucket 的后面挑选空位,用来放置 key
- 哈希表存在碰撞问题,解决方法
- 搜索树:AVL 树,和红黑树 O(logN)
- 哈希查找表 O(N)
底层原理
- map 的内存模型
// src/runtime/map.go
type hmap struct {
// 元素个数
count int
flags uint8
// buckets 的对数 log-2
B uint8
// overflow 的bucket 近似值
noerflow uint16
// hash 函数
hash0 uint32
// buckets 数组,大小为2^B
buckets unsafe.Pointer
// 扩容时,buckets 长度时 oldbuckets 的两倍
oldbuckets unsafe.Pointer
// 扩容进度,小于此地址的bucket 完成迁移
nevacuate uniptr
extra *mapextra
}
每个 bucket 中最多可以存储 8 对键值对,Go 使用数组存储这些键值对。当 bucket 的大小超过限制时,系统会进行扩容。 B 是 buckets 数组的长度的对数,buckets 是一个指针,指向一个结构体:
type bmap struct {
tophash [bucketCnt]uint8
}
// 编译后
type bmap struct {
topbits [8]uint8
keys [8]keytype
values [8]valuetype
pad uintptr
overflow uintptr
}
map 扩容过程是怎样的
触发扩容条件
map会在以下两种情况下触发扩容:
- 负载因子超过阈值 当map中已存储的元素个数超过当前bucket总数的6.5倍时,就会触发扩容。这个6.5是Go语言中经过测试得出的一个经验值。
- 溢出桶太多 当溢出桶(overflow buckets)的数量太多时也会触发扩容。具体来说,如果bucket数量小于等于15,溢出桶数量超过bucket数量就会扩容;如果bucket数量大于15,溢出桶数量超过2^15就会扩容。
扩容过程
Go语言采用了渐进式的扩容方式,而不是一次性将所有数据重新哈希。主要步骤如下:
- hashGrow函数初始化新的bucket数组 扩容时,会新建一个更大的bucket数组,bucket数量通常是原来的两倍。同时会将老的bucket数组赋值给oldbuckets字段。 evacuate函数负责数据迁移 在执行写操作(赋值、删除等)时,会通过evacuate函数将oldbuckets中的数据搬迁到新的bucket数组中。每次最多迁移两个bucket的数据。
- 增加evacuatedNodes计数 evacuatedNodes记录已迁移的bucket个数。当evacuatedNodes等于oldbuckets长度时,说明所有数据已迁移完毕。
- 清理oldbuckets 所有数据迁移完毕后,会清理oldbuckets字段,以节省内存。
总的来说,Go语言的map扩容是通过渐进式rehash实现的,避免了一次性rehash带来的延迟。同时还引入了overflow buckets来缓解rehash时数据迁移的压力。这种设计使得map的读写性能更加平滑和可控。
golang map的rehash是如何影响程序性能的
Go语言中map的rehash(重新哈希)过程会对程序性能产生一定影响,主要体现在以下几个方面:
- 一次性rehash可能导致停顿 传统的rehash方式是一次性将所有数据重新哈希到新的bucket数组中,这可能会导致程序在rehash期间出现较长时间的停顿,影响程序的响应时间和延迟。
- 渐进式rehash的额外开销 Go语言采用了渐进式的rehash方式,避免了一次性rehash带来的停顿,但也引入了一些额外的开销。在执行写操作时,需要检查是否需要rehash,如果需要则执行evacuate函数将部分数据迁移到新的bucket数组中。这些额外的检查和迁移操作会增加写操作的CPU开销。
- 内存占用暂时增加 在渐进式rehash过程中,需要同时维护新旧两个bucket数组,直到所有数据迁移完毕。这会导致map在rehash期间的内存占用暂时增加一倍左右。
- 读操作需要检查多个bucket 对于正在rehash的map,读操作可能需要查询两个bucket数组,从而增加了读操作的开销。不过这种情况相对较少见。
- rehash过程中并发访问可能导致竞争 由于rehash过程中需要读写bucket数组,如果在多个goroutine中并发访问map,可能会导致竞争条件和数据竞争问题。因此map不是线程安全的,在并发场景需要使用sync.Map或者加锁等机制。
总的来说,Go语言的渐进式rehash设计在一定程度上缓解了一次性rehash带来的延迟,但也引入了一些额外的CPU和内存开销。对于大多数应用场景,这些开销是可以接受的,rehash对整体性能的影响也是可控的。但在对延迟或内存占用要求非常严格的场景下,仍需要格外注意rehash可能带来的影响。
go map 如何解决冲突的
- 哈希计算:首先,每个键都会通过一个哈希函数进行处理,计算出一个哈希值。Golang 使用一种伪随机的哈希种子来增强哈希算法的随机性和安全性。
- 定位桶:根据计算出的哈希值,通过位操作确定键应该放置在哪个桶中。
- 遍历桶:一旦确定了桶,Go 会遍历该桶中的所有单元格(cells)。每个桶可以存储多个键值对(通常是8个)。这是通过 for i := uintptr(0); i < bucketCnt; i++ 循环完成的。
- 比较 tophash:为了快速筛选,Go 首先比较存储在 tophash 数组中的哈希值的高8位。这是一种优化,可以避免不必要的完整键比较。
- 键比较:如果 tophash 匹配,Go 会进行完整的键比较(if t.key.equal(key, k))。如果找到匹配的键,就返回对应的值。
- 溢出桶:如果在当前桶中没有找到匹配的键,且存在溢出桶,Go 会继续在溢出桶中查找。这通过 for ; b != nil; b = b.overflow(t) 循环实现。
- 插入新键值对:当插入新的键值对时,如果发生冲突(即桶已满),Go 会创建一个新的溢出桶,并将新的键值对插入到这个溢出桶中。
- 负载因子和重新哈希:为了保持良好的性能,Go 会在 map 的大小增长到一定程度时进行重新哈希(rehashing)。这个过程会创建一个更大的桶数组,并逐步将旧桶中的数据迁移到新桶中。
func mapassign(t *maptype, h *hmap, key unsafe.Pointer) unsafe.Pointer {
if h == nil {
panic("assignment to entry in nil map")
}
hash := t.key.alg.hash(key, uintptr(h.hash0))
// 定位到具体的桶
bucket := hash & ((1 << h.B) - 1)
if oldbuckets != nil {
growWork(t, h, bucket)
}
// 主桶
b := (*bmap)(add(h.buckets, bucket*uintptr(t.bucketsize)))
top := tophash(hash)
// 在主桶及溢出桶中查找键或空位
for {
for i := uintptr(0); i < bucketCnt; i++ {
if b.tophash[i] == top && t.key.equal(key, add(b.keys(), i*t.keysize)) {
// 找到键,进行赋值或返回位置
return add(b.values(), i*t.valuesize)
}
if b.tophash[i] == emptyRest {
// 找到空位,可以插入新键
b.tophash[i] = top
return add(b.keys(), i*t.keysize)
}
}
// 没有找到空位,处理溢出桶
ovf := b.overflow(t)
if ovf == nil {
// 创建新的溢出桶
ovf = h.newoverflow(t, b)
b.setoverflow(t, ovf)
}
b = ovf
}
}
数据竞态
数据竞态和内存访问冲突
在没有锁的情况下,一个 goroutine 可能正在读取一个键的值,而另一个 goroutine 同时修改同一个键或其附近的键(因为它们可能在同一个哈希桶中)。这种情况下,读操作可能遇到以下几种问题:
• 读取到部分写入的数据:如果写操作正在修改一个值,而这个值是分几步写入的(例如大型结构或多个字段),读操作可能会看到只写了一部分的数据。
• 无效的内存引用:如果写操作涉及到重新分配内存(如在扩容时),读操作可能引用了已经被释放或重新分配的内存。
Go 运行时的检测机制
从 Go 1.6 开始,Go 运行时增加了对并发访问 map 的检测。如果检测到并发读写,运行时会抛出一个 panic。这是一种保护机制,目的是防止程序在未知的、可能导致更严重问题的状态下继续运行。
底层细节:
在多核处理器环境中,各个核有自己的缓存。当对内存进行写操作时,变更可能首先在一个核的缓存中发生,稍后才通过复杂的缓存一致性协议被写回主内存。这意味着,如果一个核上的线程正在更新 map 的某个元素,而另一个核上的线程试图读取同一个 map,后者可能会看到以下情况之一:
• 已经写入缓存但未写回到主内存的数据:这可能导致读操作看到旧值。
• 部分更新的数据结构:如果写操作涉及多个步骤(例如先写键后写值),读操作可能在这些步骤完成之前发生,导致读取到不一致或不完整的数据。
- 编译器和处理器的指令重排序
编译器优化和处理器执行时的指令重排序也可能影响内存操作的实际执行顺序。例如,编译器可能重新排序某些写操作以提高效率,如果没有明确的内存屏障或锁来防止这种重排序,读操作可能会在写操作逻辑上完成之前实际发生,从而观察到不完整的数据。
interface
Go 语言中 interface 的实现源码主要包括两个核心数据结构:eface 和 iface。
eface
eface 代表空接口 interface{}。它的定义如下:
type eface struct {
_type *_type
data unsafe.Pointer
}
-
_type指向一个_type结构体,描述了该接口值的动态类型信息。 -
data是一个指针,指向该接口值的实际数据。
iface
iface 代表非空接口,比如 io.Reader。它的定义如下:
type iface struct {
tab *itab
data unsafe.Pointer
}
tab指向一个itab结构体,描述了该接口的元数据信息。data同 eface,指向实际数据。
itab
itab 结构体定义如下:
type itab struct {
inter *interfacetype
_type *_type
hash uint32
_ [4]byte
fun [1]uintptr
}
inter指向该接口自身的元数据。_type指向实际数据的类型信息。hash是类型的哈希值,用于快速比较。fun是一个函数指针数组,存储了该类型实现的接口方法。
当将一个具体类型的值赋给接口值时,编译器会根据该类型实现的方法生成一个 itab,并将其与实际数据的 _type 信息一起存储在 iface 中。这样在运行时,通过 iface.tab 就可以找到该值实现的接口方法集。
通过这种方式,Go 语言实现了接口的动态分发。当调用接口值的方法时,运行时会根据 iface.tab 找到正确的方法实现并执行。这种延迟绑定让不同类型的值可以被视为同一接口类型,实现了面向接口编程。
空接口 interface{} 的使用
var data *byte{}
var in interface{}
fmt.Println(data, data == nil) // <nil> true
fmt.Println(in, in == nil) // <nil> true
in = data
fmt.Println(in, in == nil) // <nil> false
解析: 空接口 interface{} 可以存储任何类型的值,包括 nil。当将 nil 赋值给空接口时,其底层数据仍为 nil,但其类型信息已经存在,因此 in == nil 为 false
接口值比较
// 1. type 和 data 都相等
type ProfileInt interface {}
func main() {
var p1, p2 ProfileInt = Profile{"iswbm"}, Profile{"iswbm"}
var p3, p4 ProfileInt = &Profile{"iswbm"}, &Profile{"iswbm"}
fmt.Printf("p1 --> type: %T, data: %v \n", p1, p1)
fmt.Printf("p2 --> type: %T, data: %v \n", p2, p2)
fmt.Println(p1 == p2) // true
fmt.Printf("p3 --> type: %T, data: %p \n", p3, p3)
fmt.Printf("p4 --> type: %T, data: %p \n", p4, p4)
fmt.Println(p3 == p4) // false
}
// 2. 两个都是nil
type ProfileInt interface {}
func main() {
var p1, p2 ProfileInt
fmt.Println(p1==p2) // true
}
// 3.interface 与 非interface 比较
func main() {
var a string = "iswbm"
var b interface{} = "iswbm"
fmt.Println(a==b) // true
}
func main() {
var a *string = nil
var b interface{} = a
fmt.Println(b==nil) // false
}
解析: 在 Go 中,接口值的比较并不是比较其动态值,而是比较其动态类型和动态值。上例中 x和 y 的动态类型相同,但动态值不同(不同的内存地址),因此比较结果为 false。
接口新概念(Go 1.18+)
Go 1.18 引入了一些新的接口相关概念:
- Type Set(类型集合): 接口代表的是类型的集合,而不再是方法集合。
- Specific Type(特定类型): 接口可以包含具体的类型,如
interface{int, string}。 - Structural Type(结构类型): 接口可以包含近似类型,如
interface{~string}。
编译期间检查接口实现
type CommonResponseIface interface {
GetCode() int
GetMessage() string
MergeMessage()
}
// 编译期间检查接口实现
var _ CommonResponseIface = (*CommonResponse)(nil)
type CommonResponse struct {
Code int `json:"code"` // 状态码 枚举: 200正常 500错误
Data interface{} `json:"data"` // 数据包
Message string `json:"message"` // 消息。接口返回格式不统一,这边做个兼容
Msg string `json:"msg"` // 消息。接口返回格式不统一,这边做个兼容
}
func (c *CommonResponse) GetCode() int {
return c.Code
}
func (c *CommonResponse) GetMessage() string {
if c.Message != "" {
return c.Message
}
return c.Msg
}
func (c *CommonResponse) MergeMessage() {
if c.Message == "" {
c.Message = c.Msg
}
}
channel
数据结构
Channel 的数据结构定义在 runtime/chan.go 中的 hchan 结构体中
- hchan 结构体包含以下字段:
type hchan struct { qcount uint // 队列中当前元素个数 dataqsiz uint // 循环队列的长度 buf unsafe.Pointer // 指向循环队列的指针 elemsize uint16 // 元素大小 closed uint32 // 标识 channel 是否已关闭 elemtype *_type // 元素类型 sendx uint // 下一个发送元素在 buf 中的索引 recvx uint // 下一个接收元素在 buf 中的索引 recvq waitq // 等待接收数据的 goroutine 队列(双向链表) sendq waitq // 等待发送数据的 goroutine 队列(双向链表) lock mutex // 保护 hchan 的互斥锁 } - buf 是一个循环队列,用于存储 channel 接收的数据 sendx 和 recvx 分别记录下一个可以发送和接收的元素在 buf 中的索引位置
- recvq 和 sendq 是两个双向链表,分别用于存储等待从 channel 接收数据和等待向 channel 发送数据的 goroutine lock 是一个互斥锁,用于保护 hchan 结构体中的所有字段,确保 channel 的线程安全性
- elemsize 和 elemtype 分别记录 channel 中元素的大小和类型,用于数据的拷贝和类型检查
- closed 标识 channel 是否已关闭,用于在发送和接收操作时进行检查
底层原理
Channel 本质上是由三个 FIFO(先进先出)队列组成的用于协程之间传输数据的协程安全的通道 这三个队列分别是: buf 循环队列:存放 channel 接收的数据 sendq 待发送者队列:存放等待发送数据到 channel 的 goroutine 的双向链表 recvq 待接收者队列:存放等待从 channel 接收数据的 goroutine 的双向链表
Channel 的工作原理
- 对于无缓冲的 channel,如果没有接收者准备好,发送操作会阻塞发送者 goroutine;如果没有发送者准备好,接收操作会阻塞接收者 goroutine
- 对于有缓冲的 channel,在缓冲区未满时发送操作不会阻塞,在缓冲区非空时接收操作不会阻塞。数据先写入缓冲区 buf,然后从缓冲区读取
- Channel 传递数据的本质是值拷贝,包括引用类型数据的地址拷贝。数据从发送者栈内存拷贝到缓冲区 buf,或从缓冲区 buf 拷贝到接收者栈内存
- 关闭一个 channel 会导致 panic,除非是向一个已经关闭的 channel 发送数据。关闭 channel 后,后续的发送操作会 panic,而接收操作会返回对应类型的零值和 false
- 使用无缓冲 channel 时,如果发送者和接收者不能及时配对,可能会导致 goroutine 泄漏,造成内存泄漏。可以通过使用有缓冲 channel 或在发送后关闭 channel 来避免这个问题
综上所述,Golang 的 channel 机制是基于环形队列和双向链表实现的,设计上体现了 Go 并发编程的理念"不要通过共享内存来通信,而是通过通信来共享内存"。开发者需要谨慎使用 channel,特别是无缓冲 channel,以避免出现 goroutine 泄漏等问题。
| 操作 | 通道状态 | 结果 | 解释 |
|---|---|---|---|
| 写入到 Channel | 未初始化 | panic | 向未初始化的通道写入数据将导致 panic |
| 未关闭 | 成功/阻塞 | 如果有足够的空间,写入将成功并继续运行;如果通道已满,写入操作将阻塞直到有空间或者通道被关闭;如果通道被关闭,将会 panic | |
| 已关闭 | panic | 写入操作将 panic | |
| 读取 Channel | 未初始化 | 阻塞 | 从未初始化的通道读取数据将会永远阻塞,直到通道被初始化为止 |
| 未关闭 | 成功/阻塞 | 如果有值,读取将成功并返回该值;如果没有值,读取操作将阻塞直到有值或者通道被关闭;如果通道被关闭且为空,返回默认值 | |
| 已关闭 | 默认值 | 如果有值,读取将成功并返回该值;如果没有值,立即返回默认值;如果通道被关闭且为空,返回默认值 | |
| 关闭 Channel | 未初始化 | 尝试关闭未初始化的通道将导致 panic | |
| 未关闭 | 关闭通道,后续对通道的读取操作将返回默认值 | ||
| 已关闭 | panic | 关闭通道将 panic |
defer
Go语言中defer的实现主要依赖于两个关键的数据结构:_defer和defer语句在编译期生成的defer指令。 _defer结构体 _defer是一个链表结构,用于存储延迟执行的函数信息。它的定义如下:
type _defer struct {
siz int32 // 参数大小
started bool // 是否已经执行
heap bool // 是否分配在堆上
sp uintptr // 调用方函数的sp寄存器值
pc uintptr // 调用defer的pc
fn *funval // 延迟执行的函数
_panic *_panic // 触发panic时的信息
link *_defer // 链表指针
frameCtor uintptr // 构造函数
frameData uintptr // 构造函数参数
}
其中最关键的字段是fn和link。fn存储了延迟执行函数的信息,link将多个_defer通过链表连接起来。
defer指令
当编译器遇到defer语句时,会生成相应的defer指令,用于在运行时创建_defer结构并将其链接到_defer链表中。 defer指令的执行过程大致如下:
- 计算defer语句中函数的参数值
- 创建一个_defer结构,填充相关字段
- 将新创建的_defer链接到当前goroutine的_defer链表头部
- 当函数返回时,依次从链表头部取出_defer,执行其中的fn函数
如果在执行defer函数时发生panic,则defer函数会暂时终止,等待panic处理完毕后继续执行剩余的defer函数。
defer 和 return 运行顺序
包含 defer 语句的函数返回时,先设置返回值还是先执行 defer 函数?
- 函数的调用过程 要理解这个过程,首先要知道函数调用的过程:
go 的一行函数调用语句其实非原子操作,对应多行汇编指令,包括 1)参数设置, 2) call 指令执行; 其中 call 汇编指令的内容也有两个:返回地址压栈(会导致 rsp 值往下增长,rsp-0x8),callee 函数地址加载到 pc 寄存器; go 的一行函数返回 return语句其实也非原子操作,对应多行汇编指令,包括 1)返回值设置 和 2)ret 指令执行; 其中 ret 汇编指令的内容是两个,指令 pc 寄存器恢复为 rsp 栈顶保存的地址,rsp 往上缩减,rsp+0x8; 参数设置在 caller 函数里,返回值设置在 callee 函数里; rsp, rbp 两个寄存器是栈帧的最重要的两个寄存器,这两个值划定了栈帧; 最重要的一点:Go 的 return 的语句调用是个复合操作,可以对应一下两个操作序列:
- 设置返回值
- ret 指令跳转到 caller 函数
- return 之后是先返回值还是先执行 defer 函数? Golang 官方文档有明确说明:
That is, if the surrounding function returns through an explicit return statement, deferred functions are executed after any result parameters are set by that return statement but before the function returns to its caller.
也就是说,defer 的函数链调用是在设置了返回值之后,但是在运行指令上下文返回到 caller 函数之前。
所以含有 defer 注册的函数,执行 return 语句之后,对应执行三个操作序列:
- 设置返回值
- 执行 defer 链表
- ret 指令跳转到 caller 函数
那么,根据这个原理我们来解析如下的行为:
func f1 () (r int) {
t := 1
defer func() {
t = t + 5
}()
return t
}
func f2() (r int) {
defer func(r int) {
r = r + 5
}(r)
return 1
}
func f3() (r int) {
defer func () {
r = r + 5
} ()
return 1
}
这三个函数的返回值分别是多少?
答案:f1() -> 1,f2() -> 1,f3() -> 6 。
a) 函数 f1 执行 return t 语句之后:
设置返回值 r = t,这个时候局部变量 t 的值等于 1,所以 r = 1; 执行 defer 函数,t = t+5 ,之后局部变量 t 的值为 6; 执行汇编 ret 指令,跳转到 caller 函数; 所以,f1() 的返回值是 1 ;
b) 函数 f2 执行 return 1 语句之后:
设置返回值 r = 1 ; 执行 defer 函数,defer 函数传入的参数是 r,r 在预计算参数的时候值为 0,Go 传参为值传递,0 赋值给了匿名函数的参数变量,所以 ,r = r+5 ,匿名函数的参数变量 r 的值为 5; 执行汇编 ret 指令,跳转到 caller 函数; 所以,f2() 的返回值还是 1 ;
c) 函数 f3 执行 return 1 语句之后:
设置返回值 r = 1; 执行 defer 函数,r = r+5 ,之后返回值变量 r 的值为 6(这是个闭包函数,注意和 f2 区分); 执行汇编 ret 指令,跳转到 caller 函数; 所以,f1() 的返回值是 6 ;
defer 闭包捕获的变量和常量是引用传递不是值传递
for i := 0; i < 3; i++ {
defer func() {
fmt.Println(i)
}()
}
3
3
3
for i := 0; i < 3; i++ {
item := i
defer func() {
fmt.Println(item)
}()
}
2
1
0
// 作为函数参数
for i := 0; i < 3; i++ {
defer fmt.Println(i)
}
2
1
0
func main() {
x := 10
defer fmt.Println("Deferred:", x) // x 的值在这里被捕获
x = 20 // 修改 x 的值
fmt.Println("Before defer:", x)
}
/*
Before defer: 20
Deferred: 10
*/
Panic & recover
如果在匿名函数内panic了,在匿名函数外的defer是否会触发panic-recover?反之在匿名函数外触发panic,是否会触发匿名函数内的panic-recover?
情况 1:匿名函数内的 panic,匿名函数外的 defer-recover 可以捕捉
func main() {
defer func() {
if r := recover(); r != nil {
fmt.Println("Recovered in main", r)
}
}()
func() {
panic("panic in anonymous function")
}()
}
// Recovered in main panic in anonymous function
情况 2:匿名函数外的 panic,匿名函数内的 defer-recover 程序崩溃
func main() {
func() {
defer func() {
if r := recover(); r != nil {
fmt.Println("Recovered in anonymous function", r)
}
}()
}()
panic("panic in main")
}
// panic: panic in main
// goroutine 1 [running]:
// main.main()
// /Users/alan/github/toy/go/panic_recover/xpanic.go:26 +0x30
结论:
- panic会沿调用栈向上传播
- 只有已经注册的defer函数会在panic时执行
- recover只能在defer函数中直接调用才有效
- recover 只能捕获同一个 goroutine 中的 panic。每个 goroutine 都有自己的调用栈,panic 只会沿着当前 goroutine 的调用栈传播。
- 它保持了 goroutine 之间的独立性,防止一个 goroutine 的问题直接影响其他 goroutine。
- 它简化了并发编程模型,使得每个 goroutine 的行为更加可预测。
- 它鼓励开发者在每个 goroutine 中正确处理错误和异常情况
Golang 有哪些不能recover 的panic
- 运行时错误
- 栈溢出(Stack Overflow)
- OOM
- 并发map写入
- 死锁
- 使用已关闭channel发送接收数据
- 重复panic
- defer 函数中再次panic
- 不同goroutine中发生panic
- recover 只能捕获同一 goroutine 中的 panic。
- 手动调用 os.Exit()
- 系统信号导致panic
Context
context:上下文,主要作用在 goroutine 之间传递上下文信息,包括:取消信号、超时时间、截止时间、k-v等。
Context 的底层原理
-
接口
Contexttype Context interface { // 返回 context 是否会被取消或者自动取消的时间 Deadline() // 当 context 被取消或者到 deadline 时, 返回一个被关闭的 channel Done() // channel 关闭后,返回 context 取消的原因 Err() // 获取 key 对应的 value Value() }Canceler
type canceler interface { cancel() Done() }对于实现上面定义的两个方法的 context ,就表明时可取消的。
-
结构体
- emptyCtx:实现列 Context 接口,它是一个空context,永远不会被取消,没有存储值,没有 deadline
- cancelCtx:可以被取消
- timerCtx:超时会被取消
- valueCtx:可以存储k-v对
-
函数
- CancelFunc: 取消函数
- Background: 返回空的 context,常用于根 context
- TODO:返回空的 context,常用于重构时期,没有合适的 context 可用
- WithCancel: 基于父 context,生成一个可以取消的 context
- WithDeadline: 创建一个有 deadline 的 context
- WithTimeout: 创建一个有 timeout 的 context
- WithValue: 创建一个存储 k-v 的 context
Context 的使用陷阱
- 使用
WithCancel、WithCancelCause、WithTimeout和WithDeadline函数时,一定要调用cancel函数。 - 子
goroutine一定要设置正确的检查点,及时检查 Context 是否已被撤销或者超时。
进阶篇
runtime
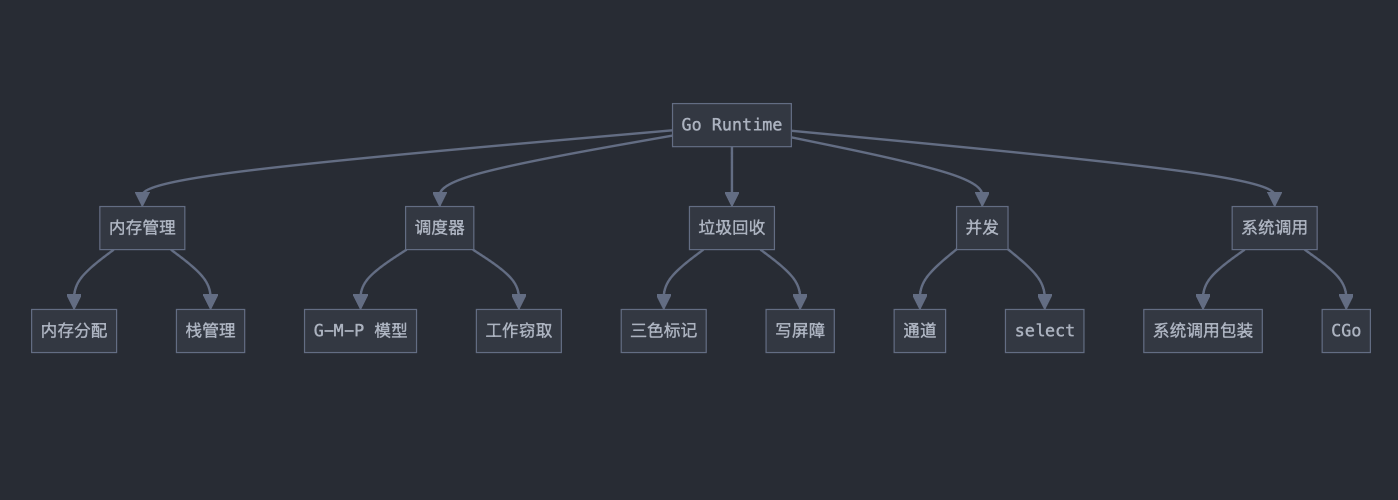
主要组成部分:
- 内存管理
-
内存分配
- 使用TCMalloc(thread-cacheing malloc)算法的变体
- 对象根据大小分为微小对象(0-16B)、小对象(16B-32KB)和大对象(>32KB)。 使用 mspan 结构管理内存页,mcache 为每个 P 提供本地缓存。 内存分配时,会优先从 线程缓存 获取,当 线程缓存 没有足够的内存时,会尝试从 中心缓存 获取,如果申请内存超过 32KB 时,会直接从 页堆 获取。
- mcentral 用于在不同 mcache 之间平衡内存。
-
栈管理
- 使用分段栈(Segmented Stacks)技术,初始栈大小通常为 2KB。
- 当栈空间不足时,会触发栈扩容,创建新的更大的栈并复制内容。
- Go 1.4 之后采用连续栈(Contiguous Stacks)来避免 "hot split" 问题。
-
调度器
-
GMP 模型
- G(Goroutine):表示一个并发任务。
- M(Machine):表示操作系统线程。
- P(Processor):表示调度上下文,用于调度 G 到 M 上执行。 通常情况下,P 的数量等于 GOMAXPROCS。
-
工作窃取(Work Stealing)算法:
- 当一个 P 的本地队列为空时,会尝试从其他 P 的队列偷取任务。
- 保证负载均衡,提高整体性能。
-
调度过程:
-
当 G 被创建或变为可运行状态时,会被放入 P 的本地队列或全局队列。
-
M 会从绑定的 P 获取 G 来执行。
-
如果 G 执行系统调用,M 会与 P 解绑,其他 M 可能会接管该 P。
-
-
垃圾回收
-
三色标记清除算法:
-
白色:潜在的垃圾对象。
-
灰色:已被标记但其引用还未被扫描的对象。
-
黑色:已被标记且其所有引用都已被扫描的对象。
-
写屏障:
- 用于在并发标记过程中确保对象不会被错误地回收。
- 包括插入写屏障和删除写屏障。
-
-
并发标记和清除:
- GC 过程大部分与用户程序并发执行,仅在某些阶段会短暂 STW(Stop The World)。
-
触发机制:
- 基于堆大小、分配速率和时间间隔等因素自动触发。
-
系统调用
- a. 系统调用包装:
- Go runtime 对操作系统的系统调用进行了封装。
- 在进行系统调用时,会解绑 M 和 P,允许其他 G 在该 P 上运行。
-
GC
Golang GC 的触发时机
Golang 的 GC 有两种触发方式:
- 主动触发: 通过调用 runtime.GC() 函数来手动触发 GC。这种方式会阻塞当前程序,直到 GC 完成。
- 被动触发: Golang 的 GC 会根据以下两种机制自动触发:
- 内存使用阈值触发: 当堆内存使用量达到上次 GC 后存活对象内存的 2 倍时,会触发新一轮 GC。这个阈值可以通过环境变量 GOGC 来调整。
- 定时触发: 如果一段时间(默认 2 分钟)内没有触发过 GC,运行时会强制触发一次 GC。
Golang GC 的实现原理
Golang 的 GC 采用了三色标记清除算法:
- 标记阶段:
- 将所有根对象(全局变量、栈上对象等)标记为"灰色"并入队。
- 从灰色对象出发,递归地将其引用的对象标记为"黑色"。
- 在标记过程中,如果发现新的对象被引用,会将其标记为"灰色"并入队。
- 清除阶段:
- 将所有未被标记为"黑色"的对象(即"白色"对象)回收。
- 将回收的内存归还给操作系统。
- Golang 的 GC 实现中还引入了写屏障(write barrier)机制,用于在标记阶段检测对象引用关系的变化,确保标记的正确性。
总的来说,Golang 的 GC 机制通过自动触发和三色标记清除算法,能够高效地管理内存,减少内存碎片,提高程序的性能和稳定性。
什么时候触发 STW
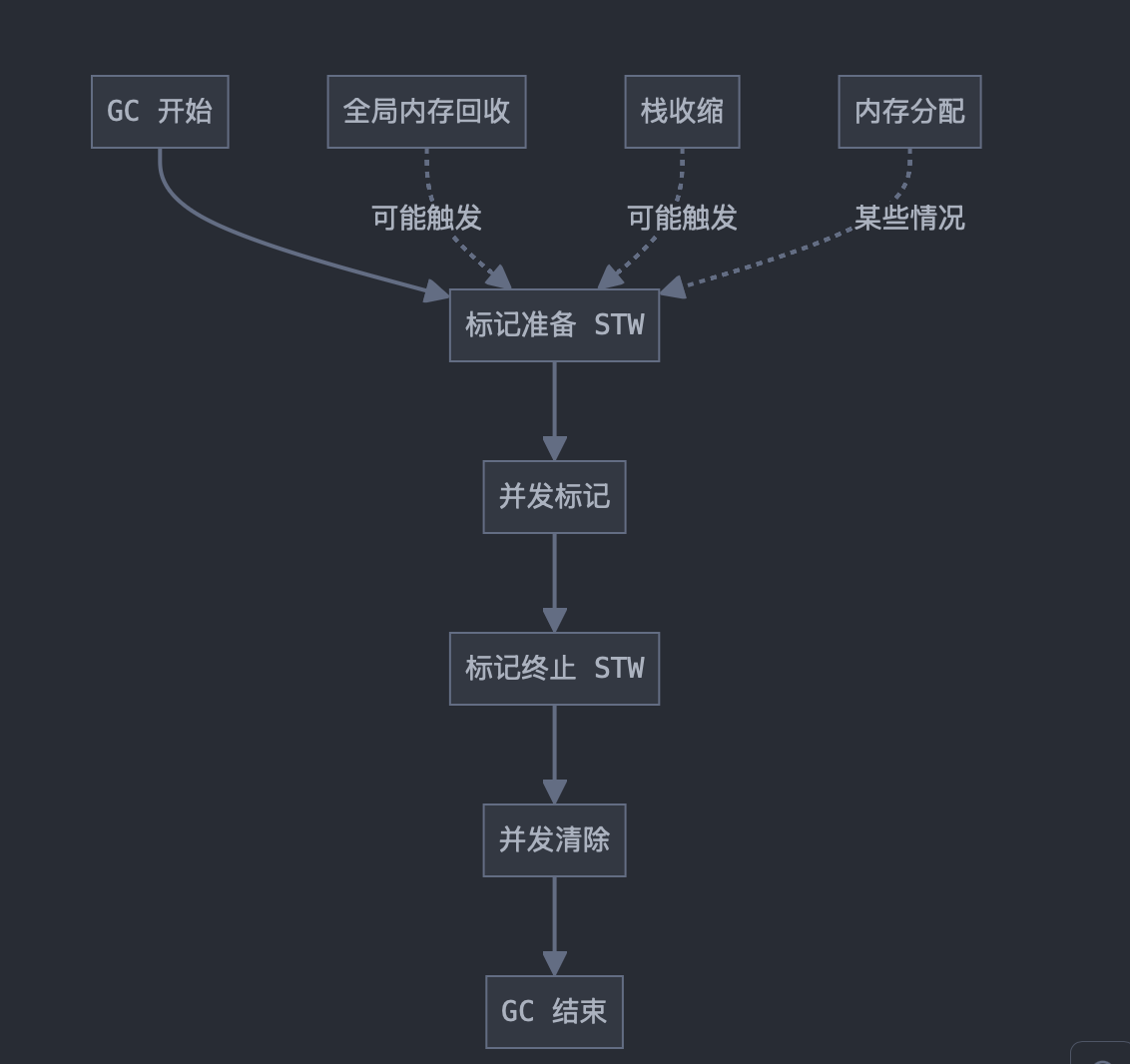
- 标记准备阶段(Mark Setup):
时机:GC 周期开始时
目的: 启用写屏障
准备 GC 工作线程
扫描所有 goroutine 的栈
持续时间:通常在 10-30 微秒级别
- 标记终止阶段(Mark Termination):
时机:并发标记阶段结束后
目的: 重新扫描(Rescan)全局队列和 P 本地队列中的对象
执行一些清理操作
关闭写屏障
持续时间:通常比标记准备阶段稍长,但仍在毫秒级别以下
非 GC 周期触发的 STW
-
全局内存回收:
时机:当需要将内存返还给操作系统时
目的:确保安全地释放不再使用的内存页
频率:相对较低,通常在程序空闲时进行 -
栈收缩(Stack Shrinking):
时机:在 GC 周期结束后,如果发现某些 goroutine 的栈使用率低
目的:减小栈的大小,释放未使用的内存
注意:这个操作通常与 GC 结合进行,以减少额外的 STW -
大对象分配:
时机:当程序尝试分配一个非常大的对象时
目的:确保有足够的连续内存空间
频率:相对较低,取决于程序的内存使用模式
STW 的触发机制
协作式抢占:Go 1.14 之前,STW 依赖于 goroutine 在特定检查点(如函数调用)自愿让出控制权 异步抢占:Go 1.14 及之后,引入了基于信号的异步抢占机制,使 STW 更加及时和可预测
减少 STW 影响的策略
-
增量 GC: Go 1.5 之后引入,将 GC 工作分散到多个小的增量中
减少了单次 STW 的持续时间 -
并行 GC: 利用多核并行执行 GC 工作
显著减少了 STW 的总时间 -
后台 GC: 在程序空闲时执行部分 GC 工作
减少了 GC 对程序性能的影响
STW 持续时间的演进
Go 1.5 之前:STW 时间可能达到几百毫秒
Go 1.5 - 1.12:STW 时间显著减少,通常在 10 毫秒以下
Go 1.13+:大多数情况下,STW 时间控制在 100 微秒量级
监控和调优
使用 GODEBUG=gctrace=1 环境变量可以查看详细的 GC 日志,包括 STW 时间
通过 pprof 工具分析 GC 性能
调整 GOGC 值可以影响 GC 频率,间接影响 STW 频率
调度器
操作系统中线程切换,涉及到上下文切换。操作系统会中断、系统调用时执行线程的上下文切换。这是一种昂贵的操作, 需要从用户态转移到内核态,保存要切换的线程的执行状态,将一些重要的寄存器的值和先查询状态保存在线程控制块数据结构中,当恢复线程运行时,再加载到集群中,从 内核态转移用户态。
goroutine 的调度由 Go 运行时可控制的,每个编译的 Go 程序都会附加一个很小的运行时,负责内存分配、goroutine 的调度和垃圾回收。 goroutine 的上下文切换可开销相对线程来说是非常小的。
- G: 表示
goroutine,存储了与goroutine相关的信息,比如栈、状态、要执行的函数等。 - P: 表示逻辑 processor, P 负责把 M 和 G 绑定在一起,让一系列的 goroutine 在 某个 M 上有序执行。
默认下 P 的数量等于 CPU 的逻辑核心数量。也可以通过
runtime.GOMAXPROCS改变 - M: 表示执行计算资源单元,Go 会把它和操作线程一一对应。只有在P和M绑定只有才能让P的本地队列中的goroutine执行起来
调度过程
- 启动一个goroutine g0
- 查找是否有空闲的P
- 如果没有就直接返回 如果有,就用系统API创建一个M(线程)
- 由这个刚创建的M循环执行能找到G任务
- G任务执行的循序 先从本地队列找,本地没有找到 就从全局队列找,如果还没有找到 就去其他P中找
- 所有的G任务的执行是按照go的调用顺序执行的
- 如果一个系统调用或者G任务执行的时间太长,就会一直占用这个线程
- (1)在启动的时候,会专门创建一个线程sysmon,用来监控和管理,在内部挨个循环
- (2)sysmon主要执行任务(中断G任务)
- 记录所有P的G任务并用schedtick变量计数,该变量在每执行一个G任务之后递增
- 如果schedtick一直没有递增,说明这个P一直在执行同一个任务
- 如果持续超过10ms,就在这个G任务的栈信息加一个标记
- G任务在执行的时候,会检查这个标记,然后中断自己,把自己添加到队列的末尾,执行下一个G
- G任务的恢复
- 中断的时候将寄存器中栈的信息保存到自己G对象里面
- 当两次轮到自己执行的时候,将自己保存的栈信息复制到寄存器里面,这样就可以接着上一次运行 goroutine是按照抢占式进行调度的,一个goroutine最多执行10ms就会换下一个
窃取
在 GMP 模型中,每个 M 都拥有一个本地队列,用于存储等待执行的 goroutine。当 M 需要执行 goroutine 时,会优先从本地队列中获取。如果本地队列为空,则会从全局队列中获取 goroutine。
为了保证全局队列中的 goroutine 能够得到公平的调度,Go 语言的调度器会每隔 61 次从全局队列中获取 goroutine 来执行。
这个数字的选择是经过考虑的。如果数字太小,则会导致全局队列中的 goroutine 得不到足够的调度机会。如果数字太大,则会导致本地队列中的 goroutine 得不到足够的调度机会。
61 是一个质数,并且与常见的 2 的幂次方(例如 64、48)不重合。这可以避免与其他调度机制发生冲突。
此外,61 也是一个相对较小的数字,这可以减少全局队列的锁竞争。
总而言之,Go 语言的调度器每隔 61 次从全局队列中获取 goroutine 来执行,是为了保证全局队列中的 goroutine 能够得到公平的调度机会。
具体来说,Go 语言的调度器会按照以下步骤执行:
从本地队列中获取 goroutine 来执行。 如果本地队列为空,则从全局队列中窃取一半的 goroutine 来执行。 如果全局队列也为空,则将 M 置于休眠状态。 每隔 61 次,调度器会跳过步骤 1,直接从全局队列中获取 goroutine 来执行。
这种调度策略可以保证全局队列中的 goroutine 能够得到公平的调度机会,同时也可以避免本地队列的锁竞争。
m0 和 g0
在 Go 语言的运行时中,g0 和 m0 是两个非常重要的对象。
g0 代表的是 main goroutine,它是 Go 程序的第一个 goroutine。g0 负责执行 main() 函数,并创建其他 goroutine。
m0 代表的是 main thread,它是 Go 程序的第一个线程。m0 负责执行 g0,并为其他 goroutine 提供调度服务。
协作式调度 和 基于信号的抢占调度
Go 1.14 之前的协作式调度主要有以下两个弊端:
无法保证 goroutine 的执行时间:如果一个 goroutine 进入死循环,则会导致其他 goroutine 无法得到执行。 无法利用多核 CPU 的全部性能:由于 goroutine 需要主动将控制权交还给调度器,因此调度器无法有效地利用多核 CPU 的全部性能。 举例子说明
无法保证 goroutine 的执行时间
func main() {
for i := 0; i < 10000; i++ {
go func() {
for {}
}()
}
// 其他 goroutine 无法得到执行
}
在这个例子中,main() 函数创建了 10000 个 goroutine,每个 goroutine 都进入了一个死循环。由于 goroutine 无法被抢占,因此其他 goroutine 无法得到执行。
无法利用多核 CPU 的全部性能
func main() {
for i := 0; i < 10000; i++ {
go func() {
time.Sleep(1 * time.Second)
}()
}
// CPU 使用率无法达到 100%
}
在这个例子中,main() 函数创建了 10000 个 goroutine,每个 goroutine 都会睡眠 1 秒。由于 goroutine 需要主动将控制权交还给调度器,因此调度器无法有效地利用多核 CPU 的全部性能。
Go 1.14 及之后的版本引入了基于信号的抢占调度,可以解决上述两个弊端。
保证 goroutine 的执行时间:当 goroutine 的运行时间超过一定时间时,调度器会向 goroutine 发送一个 SIGURG 信号,强制 goroutine 将控制权交还给调度器。 利用多核 CPU 的全部性能:调度器可以利用 SIGURG 信号来抢占 goroutine 的执行,从而提高 CPU 的利用率。 总结
Go 1.14 之前的协作式调度存在一些弊端,例如无法保证 goroutine 的执行时间和无法利用多核 CPU 的全部性能。Go 1.14 及之后的版本引入了基于信号的抢占调度,可以解决这些弊端。
什么情况下 goroutine 会被挂起
- goroutine被挂起也就是调度器重新发起调度更换P来执行时
- 在channel堵塞的时候;
- 在垃圾回收的时候;
- sleep休眠;
- 锁等待;
- 抢占;
- IO阻塞;
调度器流程图
sequenceDiagram
participant G as Goroutine
participant P as Processor (P)
participant M as Machine (M)
participant Scheduler as 调度器
G->>P: 添加到本地运行队列
P->>M: 绑定到 M(线程)
M->>P: 请求 Goroutine
P->>M: 分配 Goroutine
M->>G: 执行 Goroutine
alt Goroutine 阻塞
G->>M: 阻塞(例如系统调用)
M->>P: 通知 M 阻塞
P->>Scheduler: 寻找新的 M
Scheduler->>P: 分配新 M
P->>M': 绑定新 M
M'->>P: 请求下一个 Goroutine
P->>M': 分配 Goroutine
else Goroutine 完成
G->>M: 执行完成
M->>P: 请求下一个 Goroutine
end
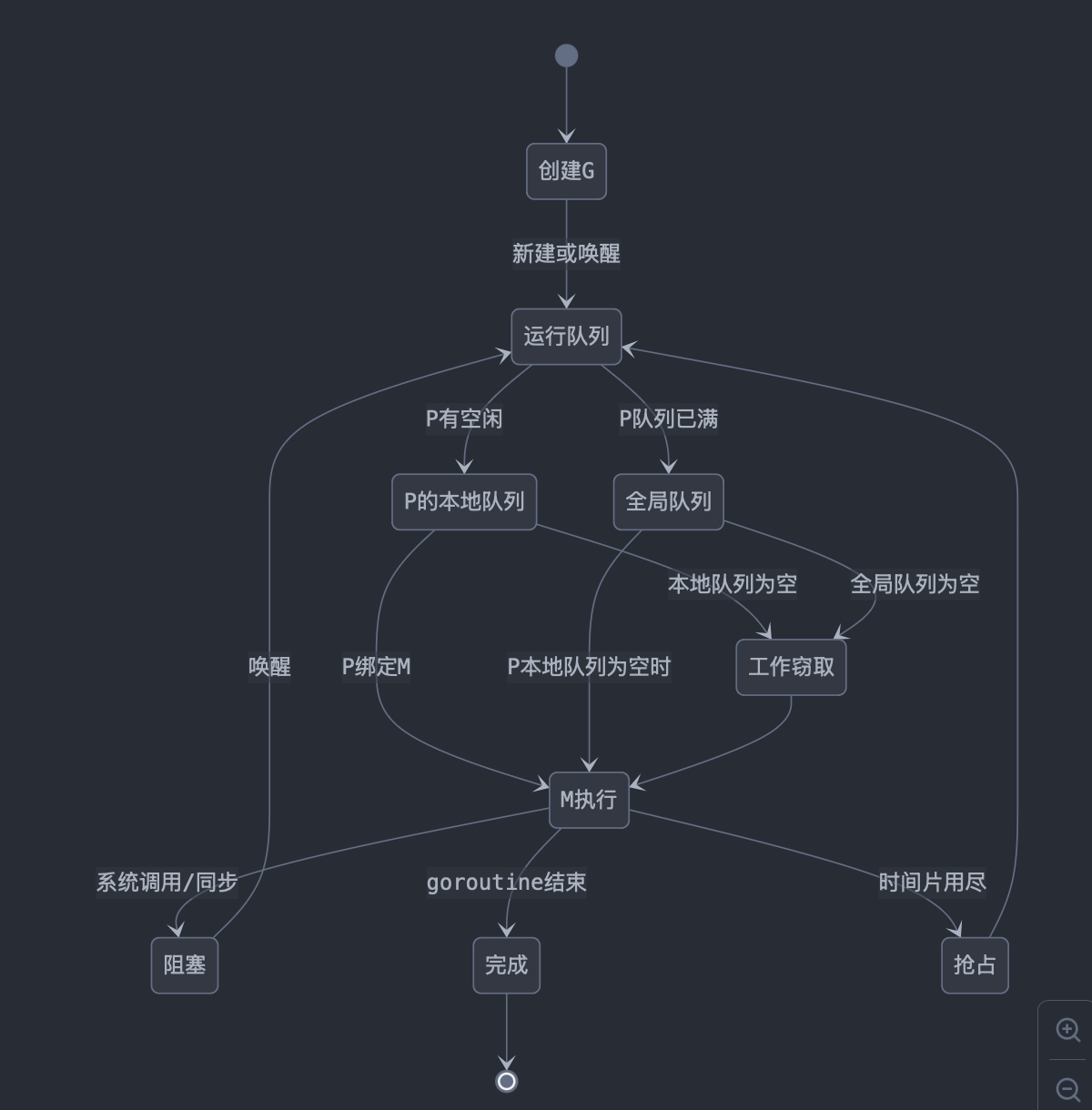
G-M-P 模型
-
G (Goroutine):表示一个并发任务,是 Go 程序中最基本的执行单元。 包含了栈、指令指针和其他调度相关的信息。 轻量级,创建和销毁的开销很小。
-
M (Machine):代表一个操作系统线程。 负责执行 G。 数量可能会随着程序的运行而动态变化。
-
P (Processor):表示一个虚拟的处理器,是 G 和 M 之间的中间层。 维护一个本地 G 队列。 数量通常等于 GOMAXPROCS 设置(默认为 CPU 核心数)。
调度流程
-
G 的创建和加入队列: 当使用 go 关键字创建新的 goroutine 时,新的 G 被创建。 新创建的 G 首先尝试加入当前 P 的本地队列。 如果本地队列已满,G 会被放入全局队列。
-
G 的执行: M 会从与之绑定的 P 的本地队列中获取 G 来执行。 如果本地队列为空,M 会尝试从全局队列或其他 P 的队列中偷取 G。
-
阻塞与唤醒: 当 G 因为系统调用或同步操作(如通道操作、互斥锁)而阻塞时,M 会与 P 解绑。 如果有空闲的 M,P 会与之绑定并继续执行其他 G。 当阻塞的 G 被唤醒时,它会重新进入 P 的本地队列或全局队列。
工作窃取(Work Stealing)算法
当一个 P 的本地队列为空时,它会尝试从其他来源获取 G:
- 从全局队列中获取 G。
- 从其他 P 的本地队列"偷"G(通常从队列尾部偷取)。
- 从网络轮询器中获取 G。
这种机制确保了负载均衡,提高了 CPU 利用率。 调度器的抢占机制
-
基于协作的抢占(Go 1.14 之前): 在函数调用时检查抢占标志。 存在无法抢占的问题,如长时间运行的 for 循环。
-
异步抢占(Go 1.14 及之后): 使用信号机制实现。 能够中断正在执行的 G,使长时间运行的 G 也能被抢占。
系统调用处理
当 G 即将进行系统调用时,M 会与 P 解绑。
- 如果系统调用是阻塞的,运行时会创建或唤醒另一个 M 来接管 P。
- 非阻塞的系统调用完成后,G 会尝试重新获取同一个 P,如果失败则进入全局运行队列。
调度器的初始化和运行
- 程序启动时,运行时会根据 GOMAXPROCS 创建 P。
- main goroutine 开始在一个 M 上运行。
- 调度器会启动一些辅助 goroutine,如 GC、监控等。
互斥锁 Mutex
底层原理
死锁
互斥锁内部流程
- mu.Lock():
- 当 Goroutine 调用 mu.Lock() 时,首先会检查这个锁的状态:
- 如果锁未被持有,则 Goroutine 成功获得锁,继续执行。
- 如果锁已经被其他 Goroutine 持有,则当前 Goroutine 被挂起,等待锁释放。
- 自旋尝试
- go.18 引入自旋锁 基本思想是,在获取锁时,如果发现锁已经被持有,线程(或 Goroutine)不会立即进入阻塞状态,而是会在一个短时间内反复尝试获取锁,这个过程称为“自旋”。自旋锁特别适用于锁持有时间很短的场景,因为它可以避免线程上下文切换带来的开销。
- 等待队列:
- 当锁被占用时,所有尝试获取锁的 Goroutine 会被放入一个等待队列中(类似于 FIFO 队列)。
- 被挂起的 Goroutine 不会消耗 CPU,Go 运行时会将这些 Goroutine 暂时停止,直到锁被释放。
- mu.Unlock():
- 持有锁的 Goroutine 调用 mu.Unlock() 释放锁时,Go 运行时会从等待队列中唤醒一个等待的 Goroutine,这个 Goroutine 会继续尝试获取锁。
- 如果没有等待的 Goroutine,锁将直接变为可用状态。
饥饿问题
在高并发争抢锁的场景中,新来的goroutine 也参与竞争,有可能每次都是被新的goroutine 获得锁的机会,在极端场景下,等待中的goroutine可能一直获取不到锁。
go1.9中 mutex 增加来饥饿模式(mutexStarving),让获取锁更加公平,不公平的等待时间限制在 1ms
饥饿模式的工作原理:
- 当一个goroutine等待锁超过1毫秒时,mutex会切换到饥饿模式。
- 在饥饿模式下,mutex的所有权会直接从解锁的goroutine转移到等待时间最长的goroutine。
- 新来的goroutine不会尝试获取锁,即使锁看起来是空闲的,它们会排到等待队列的尾部。
饥饿模式的退出:
- 当一个等待的goroutine获取了锁,并且满足以下条件之一时,mutex会退出饥饟模式:
- a) 它是队列中的最后一个等待者,或者
- b) 它等待的时间少于1毫秒
饥饿模式的优点:
- 确保了锁分配的公平性,防止了长时间的饥饿现象。
- 提高了在高并发情况下的性能表现。
Sync.Map
Golang 的 sync.Map 是一个并发安全的 map 实现,在 Go 1.9 版本中被引入。它的设计思想和底层实现如下:
设计思想
- 读写分离 sync.Map 将读和写操作分离到不同的数据结构中,避免读写冲突。读操作主要在 read 视图中进行,写操作则在 dirty 视图中进行。
- 空间换时间 sync.Map 通过冗余的数据结构(read 和 dirty),以空间换取更好的读写性能。
- 双重检查 在读取数据时,sync.Map 先检查 read 视图,如果没有则检查 dirty 视图,避免读遗漏。
- 延迟删除 删除操作只是将数据从 read 视图中标记为已删除,而不是立即从内存中删除,减少删除操作的开销。
底层实现
- 数据结构
type Map struct {
// 该锁⽤来保护dirty
mu Mutex
// 存读的数据,因为是atomic.value类型,只读类型,所以它的读是并发安全的
read atomic.Value // readOnly
//包含最新的写⼊的数据,并且在写的时候,会把read 中未被删除的数据拷⻉到该dirty中,因为是普通的map
存在并发安全问题,需要⽤到上⾯的mu字段。
dirty map[interface{}]*entry
// 一个原子操作的计数器,用于统计 read 视图读取 miss 的次数。当 misses 达到一定阈值时,sync.Map 会将 dirty 视图提升为新的 read 视图。
// 从read读数据的时候,会将该字段+1,当等于len(dirty)的时候,会将dirty拷⻉到read中(从⽽提升
读的性能)。
misses int
}
read 数据结构
type readOnly struct {
m map[interface{}]*entry
// 如果Map.dirty的数据和m 中的数据不⼀样是为true
amended bool
}
entry 数据结构
type entry struct {
//可⻅value是个指针类型,虽然read和dirty存在冗余情况(amended=false),但是由于是指针类型,存
储的空间应该不是问题
p unsafe.Pointer // *interface{}
}
sync.Map 使用 read 和 dirty 两个视图存储数据,前者用于读操作,后者用于写操作。 2. 读取流程 先在 read 视图中查找键值对,如果没有则在 dirty 视图中查找。如果 dirty 视图有新数据,则需要先将其提升(promote)到 read 视图。
func (m *Map) Load(key interface{}) (value interface{}, ok bool) {
//因read只读,线程安全,先查看是否满⾜条件
read, _ := m.read.Load().(readOnly)
e, ok := read.m[key]
//如果read没有,并且dirty有新数据,那从dirty中查找,由于dirty是普通map,线程不安全,这个时候⽤
到互斥锁了
if !ok && read.amended {
m.mu.Lock()
// 双重检查
read, _ = m.read.Load().(readOnly)
e, ok = read.m[key]
// 如果read中还是不存在,并且dirty中有新数据
if !ok && read.amended {
e, ok = m.dirty[key]
// mssLocked()函数是性能是sync.Map 性能得以保证的重要函数,⽬的讲有锁的dirty数据,
替换到只读线程安全的read⾥
m.missLocked()
}
m.mu.Unlock()
}
if !ok {
return nil, false
}
return e.load()
}
//dirty 提升⾄read 关键函数,当misses 经过多次因为load之后,⼤⼩等于len(dirty)时候,讲dirty替换到read⾥,以此达到性能提升。
func (m *Map) missLocked() {
m.misses++
if m.misses < len(m.dirty) {
return
}
//原⼦操作,耗时很⼩
m.read.Store(readOnly{m: m.dirty})
m.dirty = nil
m.misses = 0
}
- 写入流程 新的键值对直接写入 dirty 视图。当 read 视图访问次数达到阈值时,sync.Map 会将 dirty 视图中的新数据提升到 read 视图。
func (m *Map) Store(key, value interface{}) {
// 如果m.read存在这个key,并且没有被标记删除,则尝试更新。
read, _ := m.read.Load().(readOnly)
if e, ok := read.m[key]; ok && e.tryStore(&value) {
return
}
// 如果read不存在或者已经被标记删除
m.mu.Lock()
read, _ = m.read.Load().(readOnly)
if e, ok := read.m[key]; ok {
//如果entry被标记expunge,则表明dirty没有key,可添加⼊dirty,并更新entry
if e.unexpungeLocked() {
//加⼊dirty中
m.dirty[key] = e
}
//更新value值
e.storeLocked(&value)
//dirty 存在该key,更新
} else if e, ok := m.dirty[key]; ok {
e.storeLocked(&value)
//read 和dirty都没有,新添加⼀条
} else {
//dirty中没有新的数据,往dirty中增加第⼀个新键
if !read.amended {
//将read中未删除的数据加⼊到dirty中
m.dirtyLocked()
m.read.Store(readOnly{m: read.m, amended: true})
}
m.dirty[key] = newEntry(value)
}
m.mu.Unlock()
}
//将read中未删除的数据加⼊到dirty中
func (m *Map) dirtyLocked() {
if m.dirty != nil {
return
}
read, _ := m.read.Load().(readOnly)
m.dirty = make(map[interface{}]*entry, len(read.m))
//read如果较⼤的话,可能影响性能
for k, e := range read.m {
//通过此次操作,dirty中的元素都是未被删除的,可⻅expunge的元素不在dirty中
if !e.tryExpungeLocked() {
m.dirty[k] = e
}
}
}
//判断entry是否被标记删除,并且将标记为nil的entry更新标记为expunge
func (e *entry) tryExpungeLocked() (isExpunged bool) {
p := atomic.LoadPointer(&e.p)
for p == nil {
// 将已经删除标记为nil的数据标记为expunged
if atomic.CompareAndSwapPointer(&e.p, nil, expunged) {
return true
}
p = atomic.LoadPointer(&e.p)
}
return p == expunged
}
//对entry 尝试更新
func (e *entry) tryStore(i *interface{}) bool {
p := atomic.LoadPointer(&e.p)
if p == expunged {
return false
}
for {
if atomic.CompareAndSwapPointer(&e.p, p, unsafe.Pointer(i)) {
return true
}
p = atomic.LoadPointer(&e.p)
if p == expunged {
return false
}
}
}
//read⾥ 将标记为expunge的更新为nil
func (e *entry) unexpungeLocked() (wasExpunged bool) {
return atomic.CompareAndSwapPointer(&e.p, expunged, nil)
}
//更新entry
func (e *entry) storeLocked(i *interface{}) {
atomic.StorePointer(&e.p, unsafe.Pointer(i))
}
- 删除流程 删除操作只是将数据从 read 视图中标记为已删除,而不会立即从内存中删除,减少删除操作的开销。
func (m *Map) Delete(key interface{}) {
read, _ := m.read.Load().(readOnly)
e, ok := read.m[key]
//如果read中没有,并且dirty中有新元素,那么就去dirty中去找
if !ok && read.amended {
m.mu.Lock()
//这是双检查(上⾯的if判断和锁不是⼀个原⼦性操作)
read, _ = m.read.Load().(readOnly)
e, ok = read.m[key]
if !ok && read.amended {
//直接删除
delete(m.dirty, key)
}
m.mu.Unlock()
}
if ok {
//如果read中存在该key,则将该value 赋值nil(采⽤标记的⽅式删除!)
e.delete()
}
}
func (e *entry) delete() (hadValue bool) {
for {
p := atomic.LoadPointer(&e.p)
if p == nil || p == expunged {
return false
}
if atomic.CompareAndSwapPointer(&e.p, p, nil) {
return true
}
}
}
综上所述,sync.Map 通过读写分离、空间换时间、双重检查和延迟删除等优化策略,实现了高性能的并发安全 map。但对于频繁增删的场景,其性能可能不如使用 sync.RWMutex 加锁的方式
性能对比
-
sync.map
- 读多写少
- sync.Map 的结构优化了读取操作,适合在数据被频繁读取但不常更新的场景中使用。例如,缓存数据或配置值的存储。
- 数据只增不减的情况
- 在某些情况下,数据只会增加而不会减少,sync.Map 的性能表现会更优,因为写入操作不会频繁导致锁竞争。
- 高并发访问
- 对于多个 goroutine 同时访问的情况,sync.Map 能够有效减少锁的争用,提供更好的性能。
- 读多写少
-
map 加锁
- 写操作频繁
- 当需要频繁写入数据时,使用 sync.Mutex 或 sync.RWMutex 可以更好地控制并发,尽管会引入锁的开销,但在写操作较多的情况下,性能会更稳定。
- 复杂的读写逻辑
- 如果需要在读写操作中进行复杂的逻辑处理,使用加锁的 map 可以更灵活地控制并发行为。
- 数据一致性要求高
- 在需要严格保证数据一致性的场景中,使用加锁的方式可以确保在读写操作中不会出现数据不一致的问题
- 写操作频繁
-
分段锁(concurrent-map)
-
性能对比
- 读性能 sync.Map 在读操作上表现优越,特别是在高并发的读场景中,能够通过原子操作和读缓存机制提供快速访问。
- 写性能 sync.Map 的写性能相对较差,尤其是在频繁写入的情况下,可能导致性能下降,因为写操作需要加锁,且会影响到读操作的效率。
- 锁竞争 使用 sync.Mutex 或 sync.RWMutex 的 map 在写操作时会引入锁竞争,可能导致性能瓶颈,尤其在高并发环境下。
- 适用性 sync.Map 更适合于读多写少的场景,而加锁的 map 则在写操作频繁的情况下表现更好.
singleflight
工作原理
- 当多个 goroutine 同时调用 Do 方法时,只有第一个会真正执行函数 fn。
- 后续的调用会等待第一个调用完成,然后直接返回结果。
- 使用 sync.WaitGroup 来同步等待。
- 使用 sync.Mutex 来保护共享的 map。
底层实现
type Group struct {
mu sync.Mutex // 保护 m
m map[string]*call // 懒加载
}
type call struct {
wg sync.WaitGroup
val interface{}
err error
dups int
}
- Group 结构体使用一个 map 来存储正在进行的调用。
- call 结构体表示一个正在进行的函数调用。
Do 方法
func (g *Group) Do(key string, fn func() (interface{}, error)) (interface{}, error, bool) {
g.mu.Lock()
if g.m == nil {
g.m = make(map[string]*call)
}
if c, ok := g.m[key]; ok {
c.dups++
g.mu.Unlock()
c.wg.Wait()
return c.val, c.err, true
}
c := new(call)
c.wg.Add(1)
g.m[key] = c
g.mu.Unlock()
g.doCall(c, key, fn)
return c.val, c.err, c.dups > 0
}
使用场景
- 标准库 net/lookup.go, 如果多个请求查询同一个 host, lookGroup 会合并请求,只请求一次就行
- 缓存失效后的重新加载
- 并发请求的合并
- 避免重复计算
定时器的实现
Go的定时器基于小顶堆(heap)数据结构和Goroutine 机制来高效管理定时任务。定时器的核心思想是尽可能减少不必要的轮询,并且利用堆来保持定时任务的有序性
- 定时器的核心数据结构 Golang 定时器的核心数据结构位于 runtime 包内,关键结构体包括:
- runtimeTimer:定时器的底层数据结构,描述了每个定时任务的属性。
- when: 任务应当触发的时间点(以纳秒为单位)。
- period: 如果是周期性任务,表示间隔时间;否则为零。
- f: 定时器触发时的回调函数。
- arg: 传递给回调函数的参数。
- status: 表示定时器的当前状态(激活、停止等)。
- timerHeap:小顶堆数据结构,用来管理所有定时器。堆按 when 排序,最早触发的定时器在堆顶。
- time.Timer 和 time.Ticker
- time.Timer:用于管理一次性定时任务,在指定时间点触发任务并执行回调。
- time.Ticker:用于管理周期性定时任务,定期触发任务并执行回调。
两者的底层实现非常类似,都是基于 runtimeTimer,区别在于 Ticker 在每次触发任务后会重新计算下一次触发时间并继续使用。
sleep 的实现
我们通常使用 time.Sleep(1 * time.Second) 来将 goroutine 暂时休眠一段时间。sleep 操作在底层实现也是基于 timer 实现的。代码在 runtime/time.go#L84。有一些比较有意思的地方,单独拿出来讲下。 我们固然也可以这么做来实现 goroutine 的休眠:
timer := time.NewTimer(1 * time.Seconds)
<-timer.C
但 golang 底层显然不是这么做的,因为这样有两个明显的额外性能损耗。 每次调用 sleep 的时候,都要创建一个 timer 对象。 需要一个 channel 来传递事件。
既然都可以放在 runtime 里面做。golang 里面做的更加干净:
- 每个 goroutine 底层的 G 对象上,都有一个 timer 属性,这是个 runtimeTimer 对象,专门给 sleep 使用。当第一次调用 sleep 的时候,会创建这个 runtimeTimer,之后 sleep 的时候会一直复用这个 timer 对象。
- 调用 sleep 时候,触发 timer 后,直接调用 gopark,将当前 goroutine 挂起。
- timerproc 调用 callback 的时候,不是像 timer 和 ticker 那样使用 sendTime 函数,而是直接调 goready 唤醒被挂起的 goroutine。
- 这个做法和libco的poll实现几乎一样:sleep时切走协程,时间到了就唤醒协程。
func timeSleep(ns int64) {
if ns <= 0 {
return
}
gp := getg()
t := gp.timer
if t == nil {
t = new(timer)
gp.timer = t
}
t.f = goroutineReady
t.arg = gp
t.nextwhen = nanotime() + ns
if t.nextwhen < 0 { // check for overflow.
t.nextwhen = maxWhen
}
gopark(resetForSleep, unsafe.Pointer(t), waitReasonSleep, traceBlockSleep, 1)
}
反射
1.为什么JSON包不能导出私有变量的tag? encoding/json 包不能导出私有字段的根本原因在于 Go 的访问控制规则。Go 语言通过首字母的大小写来控制字段和方法的可见性: - 首字母大写的字段和方法是导出的,可以被其他包访问。 - 首字母小写的字段和方法是未导出的,只能在当前包内访问。 encoding/json 包依赖于 Go 的反射机制来访问结构体字段并进行序列化和反序列化。反射机制的设计遵循 Go 的访问控制规则,即反射只能访问导出的字段。由于私有字段是未导出的,因此 encoding/json 包无法通过反射来访问它们,导致无法将私有字段进行序列化。
逃逸分析
逃逸分析,就是一些变量或对象在函数调用过程中没有被分配到栈内存,而被分配到堆内存上。简单来说就是这些变量在函数调用结束的时候没有被销毁,因为某些原因保留在堆内存上,导致内存使用可能不符合预期。 内存逃逸:当 Go 的编译器发现一个局部变量在函数结束后仍然会被使用(比如它的引用被传递到其他地方),它就无法将这个变量分配到栈上,只能分配到堆上。这就是“内存逃逸”。
举个例子 假设你有一个函数创建了一个局部变量,并返回它的引用。如果编译器发现这个返回的引用在函数调用结束后仍然会被使用,那么它就会将这个局部变量分配到堆上,而不是栈上。这样可以确保这个变量在函数返回后仍然有效,但也会导致更多的内存分配和垃圾回收开销。
后果 内存逃逸会导致更高的内存开销和更频繁的垃圾回收,因为堆上的内存需要更多的管理和维护。理解并优化内存逃逸现象可以帮助提高程序的性能和效率
栈和堆的区别:
- 栈是一个临时的内存区域,用于存储函数的局部变量,函数调用结束后这些变量会自动释放。
- 堆是一个长期的内存区域,用于存储需要长期存在的数据,必须手动管理释放。
场景
返回函数内部变量的引用:
func createClosure() *int {
x := 10
return &x // 返回局部变量的指针
}
闭包
func makeIncrementer(start int) func() int {
count := start
return func() int {
count++
return count
}
}
将局部变量传递到 Goroutine 中:
func startGoroutine() {
x := 10
go func() {
fmt.Println(x) // 在 Goroutine 中使用局部变量
}()
}
反射和接口: 使用反射(reflect 包)或接口(interface)时,编译器可能无法确定数据的实际类型或大小,因此会将数据分配到堆上,以便在运行时动态管理。
func printValue(v interface{}) {
fmt.Println(v) // 使用接口类型,可能导致数据逃逸到堆
}
How CompareAndSwap it works?
Parameters:
addr: a pointer to anint32variableoldval: the expected value of theint32variablenewval: the new value to be stored in theint32variable
Return value:
swapped: a boolean indicating whether the swap was successful (i.e., the value was updated)
How it works:
- The function loads the current value of the
int32variable pointed to byaddrinto a register. - It compares the loaded value with the
oldvalparameter. If they match, it proceeds to step 3. - It stores the
newvalparameter in theint32variable pointed to byaddr. - It returns
trueif the swap was successful (i.e., the value was updated), andfalseotherwise.
Here's an example of how you might use CompareAndSwapInt32:
package main
import (
"fmt"
"sync/atomic"
)
var counter int32
func main() {
for i := 0; i < 10; i++ {
if atomic.CompareAndSwapInt32(&counter, 0, 1) {
fmt.Println("Counter incremented successfully")
} else {
fmt.Println("Counter not incremented (another goroutine got there first)")
}
}
}
Here are some reasons why atomic.CompareAndSwap functions are concurrency-safe:
- Memory barriers: The atomic package uses memory barriers to ensure that the CPU cache is updated correctly. This prevents the CPU from caching the old value of the variable, which could lead to incorrect results.
- Lock-free: The atomic package uses lock-free algorithms to update the variables. This means that the operations are not blocked by locks, which can lead to contention and performance issues in concurrent programs.
- Atomic operations: The atomic package provides atomic operations that are designed to be executed atomically. This means that the operations are executed as a single, uninterruptible unit, which ensures that the variables are updated correctly even in the presence of concurrent access.
- Synchronization: The atomic package provides synchronization primitives, such as CompareAndSwap, that are designed to be used in concurrent programs. These primitives provide a way to synchronize access to shared variables, which ensures that the variables are updated correctly even in the presence of concurrent access.
高CPU/高内存问题排查场景
高CPU
- 业务类型问题
- 死循环
- 死锁
- 大量计算密集型任务
- 图像处理
- 视频转码
- 大量并发线程
- 内存不足
- 频繁GC(内存不足,导致频繁GC)
高内存
- 内存泄漏
- 大量文件上传/下载
工具使用
- pprof
- 火焰图观察
- 使用 go tool pprof 来分析:
go tool pprof http://localhost:6060/debug/pprof/profile?seconds=30
-- 分析堆内存
go tool pprof http://localhost:6060/debug/pprof/heap
在生成的 pprof 交互式界面中,可以使用命令如 top、list 和 web 来查看热点函数和调用图。 2. 分析 Goroutine 状态: 高 CPU 使用可能由过多的 Goroutine 引起。可以使用 pprof 或 runtime/pprof 包获取 Goroutine 的快照:
go tool pprof http://localhost:6060/debug/pprof/goroutine
- 检查锁竞争: 如果程序中的并发部分存在锁竞争,会导致 CPU 利用率过高。可以通过 pprof 生成的锁分析报告进行检查
go tool pprof http://localhost:6060/debug/pprof/block
- 检查内存泄漏:
- 内存泄漏会导致程序的内存使用不断增长。使用 pprof 可以帮助识别是否存在内存泄漏。
- 在程序中记录堆快照,并分析内存分配情况,找出是否有未释放的对象或数据结构。
- 优化内存使用:
- 检查是否有不必要的数据存储在内存中,考虑使用更高效的内存管理策略。
- 使用内存池(sync.Pool)来减少内存分配和释放的开销。
- 分析程序中的大对象和长寿命对象:
- 查找大对象(如大切片、映射、结构体)以及长寿命对象(生命周期很长的对象),它们可能导致内存使用过高。
- 调优 GC 设置:
- 在一些情况下,GC(垃圾回收)设置可能影响内存使用。可以通过调整 GOGC 环境变量来控制 GC 的频率:
export GOGC=100
火焰图使用
火焰图的基本结构
- X 轴(横轴):
• 表示调用栈的深度或不同函数在调用栈中的位置。
• 从左到右显示函数调用的层次结构,每个矩形的宽度表示该函数占用的时间。 - Y 轴(纵轴):
• 表示函数调用的深度,栈的深度越大,函数的位置越高。
• 通常,Y 轴的上部表示栈的顶部,即调用栈的最上层,底部则表示栈的最底层。 - 矩形:
• 每个矩形代表一个函数调用。矩形的宽度表示该函数在火焰图上占据的时间(或占用的内存),越宽表示函数消耗的时间越长。
• 矩形的颜色通常表示不同的函数或模块,但颜色的具体含义可能取决于具体的火焰图工具。
阅读火焰图的步骤
- 定位宽矩形:
• 关注图中最宽的矩形,它们表示消耗时间最多的函数。这些函数可能是性能瓶颈的主要来源。 - 查看函数调用链:
• 从底部(调用栈的底层)向上查看函数调用链。每个函数都可能调用其他函数,火焰图帮助你识别哪些函数被频繁调用或时间占用较多。 - 分析函数层级:
• 识别调用链中的热点区域。函数调用的深度和广度会影响整体性能,高度层次上的函数往往是性能的关键点。 - 识别函数之间的关系:
• 通过观察函数间的调用关系,找出是否有不必要的嵌套调用或重复调用,导致时间浪费。 - 比较不同的快照:
• 如果可能,比较不同时间点或不同负载下生成的火焰图,识别性能变化的模式。
示例火焰图分析
- 宽矩形:如果你看到一个矩形很宽,表示这个函数的执行时间较长。检查这个函数是否在代码中频繁调用。
- 顶部的矩形:顶部的矩形是最上层函数调用,它们可能有很多子调用。查找这些函数,看看它们是否有可以优化的地方。
- 高深度的矩形:如果某些矩形位于较高的层次,表示它们在调用链的较深处。分析这些函数,检查是否有深层次的递归或复杂逻辑。
多个协程交替打印ABC
package main
import (
"fmt"
"sync"
)
var wg sync.WaitGroup
func main() {
Ach := make(chan int, 1)
Bch := make(chan int)
Cch := make(chan int)
wg.Add(3)
go fn("A", Ach, Bch)
go fn("B", Bch, Cch)
go fn("C", Cch, Ach)
wg.Wait()
close(Ach)
close(Bch)
close(Cch)
}
func fn(str string, ch1 chan int, ch2 chan int) {
defer wg.Done()
for i := 0; i < 10; i++ {
ch1 <- 1
fmt.Println(str, i+1)
<-ch2
}
}
注意:A协程是带缓冲的,否则会导致死锁
基础篇
基本概念
主键、索引、外键
- 主键是一列,其值可以唯一标识表的每一行数据,每个表只能一个主键,主键不能重复,也不能包含NULL值。
- 索引没有重复值,但可以有空值,用于快速查询数据
- 外键是表中一字段,其值是另一个表的主键,用于建立两表之间关系
三大范式
连接
将各个表的记录拉取出来进行依次匹配,将匹配的结果发给客户端
笛卡尔积:连接查询的结果中包含一个表的每一条记录与另一表的记录的组合,这样的查询结果就是笛卡尔积。 例如:表1有5条记录,表2有6条记录,ab表的笛卡尔积就是30。
连接过程:
- 确定第一个需要查询的表,此表就是驱动表
- 从驱动表中取出每一条符合搜索条件的记录,到接下来的表查询匹配的记录,驱动表之后的那个表就是被驱动表
- 只需要访问启动表一次,可能会多次访问被驱动表
内连接:驱动表中的记录在被驱动表中找不到的记录,那么驱动表的这条记录不会加到最后结果中。 外连接:驱动表的中记录在被驱动表中找不到的记录,仍需要加到最后结果中。
where: 无论内外连接,不符合where 子句的记录不会加到最后结果中 on:在内连接中与where 等价。在外连接中如果驱动表中记录在被驱动表中没有记录匹配,该驱动表记录仍会加到结果中,对应的被驱动表字段以null填充
查询语句是如何执行的
- 连接:客户端与服务器连接,通过mysql 连接器(权限判断)
- 建立连接复制,使用长连接
- 长连接过多,导致OOM。可定期断开,通过
mysql_reset_connection字段重新初始化连接
- 查询缓存:
- 执行查询语句前,先查询缓存是否有结果。如果有,直接取出返回,没有命中,执行查询语句,并且吧结果放入缓存
- mysql8.0开始,执行查询语句,不会再走查询缓存阶段(这是因为查询缓存在高并发环境下会带来显著的性能问题,导致系统性能下降。查询缓存需要不断地维护和刷新,在数据修改频繁的情况下,这会带来很大的开销。)
常用函数
字符集&排序规则
版本兼容
索引
索引分类
- 数据结构分类
- B+ 树索引:多用于关系型数据库索引。所有记录存在在叶子节点,并且叶子节点构成一个有序的链表,因此对范围查询有较好的性能。
- 哈希索引:基于哈希表实现,适合等值查询。
- R 树索引:常用于地理位置查询。空间索引
- 物理存储分类
- 聚簇索引:表中的数据行物理存储顺序和索引顺序一直,每个表只能有一个聚簇索引,主键即是聚簇索引。
- 非聚簇索引:索引和数据分开存储,索引中存储的是指向数据的指针。适合频繁查询操作
- 字段特性分类
- 唯一索引:索引列必须唯一,但允许一个null值
- 普通索引:没有唯一性要求
- 全文索引:针对文本内容进行分词索引,适合大文本查询
- 前缀索引:只索引字段前缀部份,适合长字符串字段,如URL、邮件等,可以节省空间
索引原理
B+数结构
索引优化
事务
事务隔离级别
mvcc
幻读&如何解决幻读
重复读
并发控制
- 锁
- mvcc
锁
锁分类
- 表级锁(锁定整个表)
- 页级锁(锁定一页)
- 行级锁(锁定一行)
- 共享锁(S锁,MyISAM 叫做读锁)
- 排他锁(X锁,MyISAM 叫做写锁)
- 间隙锁(NEXT-KEY锁)
- 悲观锁(抽象性,不真实存在这个锁)
- 乐观锁(抽象性,不真实存在这个锁)
日志
bin log
格式
- 基于语句格式
- 日志文件较小:因为记录的是 SQL 语句而不是每行数据的变化,日志文件相对较小。
- 无法精确复制某些语句:某些包含非确定性函数(如 UUID()、NOW() 等)的语句在复制时可能无法保证一致性。
- 复杂语句的复制问题:复杂语句(如包含子查询或用户自定义函数的语句)在复制时可能出现问题。
- 基于行格式
- 精确复制:记录每一行数据的变化,确保数据的一致性,即使是复杂的 SQL 语句也能准确复制。
- 日志文件较大:记录每一行数据的变化,日志文件相对较大,占用更多的存储空间。
- 难以阅读和理解:日志中记录的是数据行的变化,不如 SQL 语句直观,调试和审计较为困难。
- 混合日志
- 默认使用基于语句的日志,遇到需要精确复制的情况(如非确定性函数)时切换到基于行的日志,兼顾了两者的优点。
主从同步是如何实现的
binlog 刷盘时机
buffer pool
redo log
undo log
relay log
主从复制
基本原理
如何实现高可用
主从延迟
读写分离
半同步复制
GTID 复制
mysql排序是如何实现的
- rowid 排序
- 全字段排序
Explain 分析
字段说明
sql 分析
慢sql优化
索引下推
索引下推(Index Condition Pushdown)是数据库查询优化的一种技术,它可以在索引扫描阶段就完成一些过滤操作,从而减少需要访问的数据量,提高查询效率。
基本原理
当数据库查询包含过滤条件(如 WHERE 子句)时,传统的做法是从存储引擎读取全部数据,然后在数据库服务器层面进行过滤。 而索引下推则会将这些过滤条件尽量推到存储引擎层,由存储引擎在数据检索阶段直接过滤掉不符合条件的记录。
- 在索引扫描阶段就利用这些额外的列信息来过滤数据
- 减少需要回表(访问主表)的次数
例子
SELECT * FROM users WHERE name LIKE 'Zhang%' AND age > 30;
-- 在name列上创建了一个索引
没有使用索引下推的过程:
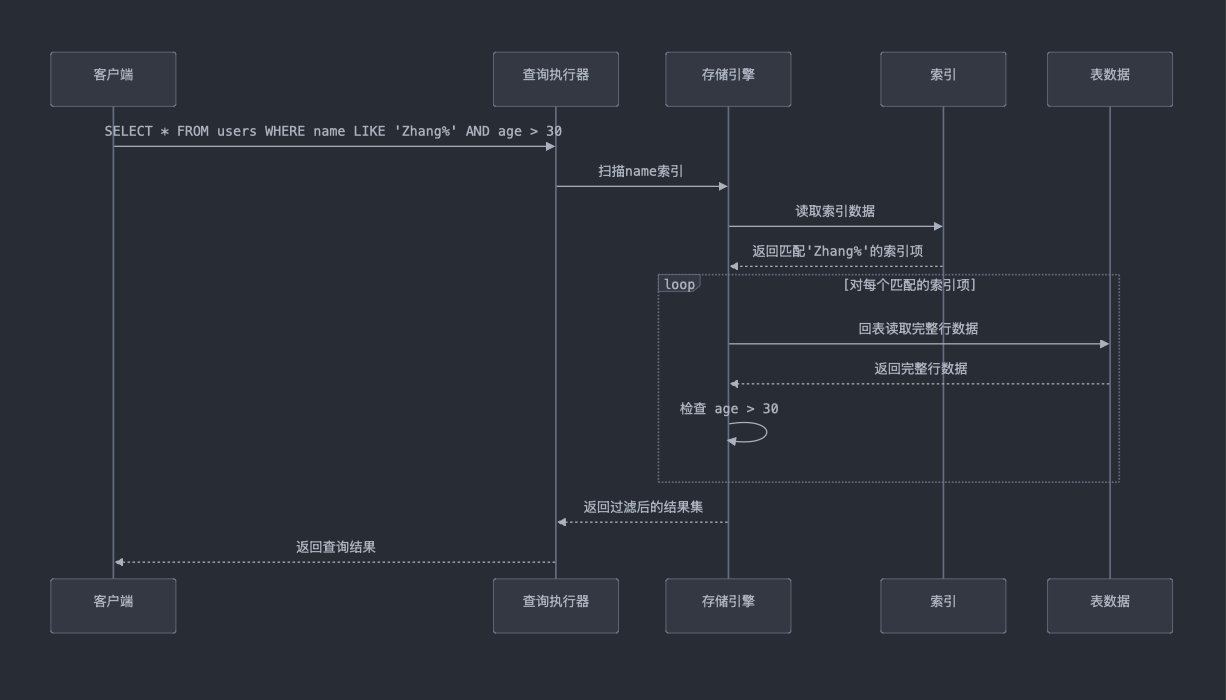
- 步骤1:索引扫描:数据库会利用 name 列上的索引,找到所有匹配前缀 'Zhang%' 的记录。在这一阶段,索引会定位到所有符合 name LIKE 'Zhang%' 的记录。
- 步骤2:回表操作:找到匹配 name 前缀的记录之后,数据库需要进行回表(通过索引找到对应的行,再去表中取完整的数据),并获取每条记录的 age 列数据。
- 步骤3:过滤:在服务器层对每条记录进行过滤,将 age > 30 的条件应用于查询结果。这意味着数据库会把所有匹配 name LIKE 'Zhang%' 的记录都读入内存,然后在内存中执行 age > 30 的过滤。
- 缺点:由于没有索引下推,所有匹配 name 条件的记录都需要进行回表操作,即便它们的 age 不符合条件也会被加载,这增加了I/O操作和内存消耗。
使用索引下推的过程:
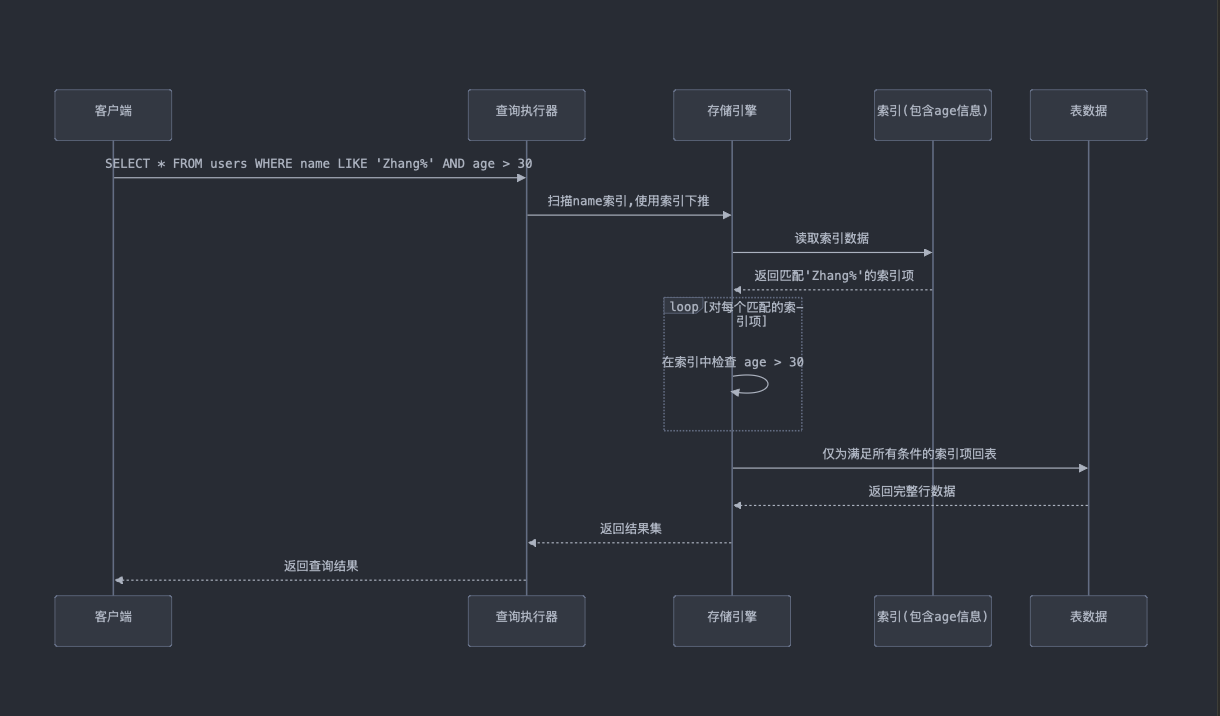
- 步骤1:索引扫描:同样,数据库首先会利用 name 列上的索引,找到所有匹配 name LIKE 'Zhang%' 的记录。
- 步骤2:索引下推:在存储引擎层面,数据库在扫描索引记录时直接应用 age > 30 的条件。也就是说,在索引扫描的过程中,只有那些 age 大于 30 的记录才会进一步处理。这减少了回表操作的次数,因为只有符合 name LIKE 'Zhang%' 且 age > 30 的记录会被回表并提取完整数据。
- 步骤3:回表操作:只有满足两个条件的记录(name LIKE 'Zhang%' 和 age > 30)才会触发回表操作,这减少了 I/O 开销和内存使用。
- 优势:索引下推通过将 age > 30 条件提前到索引扫描阶段,使得在扫描时就可以过滤掉不必要的记录,从而减少了不必要的回表操作,显著提高了查询效率。
索引下推的优势
- 减少数据传输量:因为过滤条件在存储引擎就已经应用,减少了服务器端需要处理的记录数。
- 提高查询效率:尤其是对于复杂的查询条件,索引下推能显著减少数据扫描量,提高查询的响应速度。
不走索引场景
- 索引列参与计算
SELECT `sname` FROM `t_stu` WHERE `age`=20; -- 会使用索引 SELECT `sname` FROM `t_stu` WHERE `age`+10=30; -- 不会使用索引!!因为所有索引列参与了计算 SELECT `sname` FROM `t_stu` WHERE `age`=30-10; -- 会使用索引 - 索引列使用函数
SELECT `sname` FROM `stu` WHERE concat(`sname`,'abc') ='Jaskeyabc'; -- 不会使用索引,因为使用了函数运算,原理与上面相同
SELECT sname FROM stu WHERE sname=concat('Jaskey','abc'); -- 会使用索引
```
-
索引列使用了Like %XXX
-
使用 OR 连接的条件可能导致索引失效。如果 OR 的两边没有索引,或者只有一边有索引,通常不会走索引
-
类型隐式转换,会导致全表扫描
-
不等于比较(比如时间字段) 当查询条件为字符串时,使用”<>“或”!=“作为条件查询,有可能不走索引,但也不全是,当查询结果集占比比较小时,会走索引,占比比较大时不会走索引。此处与结果集与总体的占比有关。
-
is not null 查询条件使用is null时正常走索引,使用is not null时,不走索引。
-
order by导致索引失效 当查询条件涉及到order by、limit等条件时,是否走索引情况比较复杂,而且与Mysql版本有关,通常普通索引,如果未使用limit,则不会走索引。order by多个索引字段时,可能不会走索引。其他情况,建议在使用时进行expain验证。 ORDER BY的索引优化。如果一个SQL语句形如: SELECT [column1],[column2],…. FROM [TABLE] ORDER BY [sort]; 在[sort]这个栏位上建立索引就可以实现利用索引进行order by 优化。
-
not in和not exists (非主键时,索引失效)
一条查询语句是如何工作的?
mysql 的架构分为两层:Server 层和 存储引擎层
- server 层: 负责建立连接和分析、执行sql
- 引擎层:负责数据的提取和存储
- 连接器
- 管理连接和权限验证
- Mysql 会定期⾃动清理"空闲"连接,由参数 wait_timeout 控制的,默认值是 8 ⼩时。
- 由于建⽴连接⽐较复杂,所以尽量使⽤⻓连接,⽽不是 短连接(少量查询后,就断开连接),但是,当 ⻓连接 过多时,可能导致内存占⽤太⼤,被系统强⾏杀掉(OOM),会导致 MySQL 异常重启
- 查询缓存
- 执⾏查询语句前,先看下查询缓存中是否有结果
- 不建议使⽤查询缓存(当 数据表频繁更新时,最新查询结果可能和查询缓存中存放的结果不⼀致)
- MySQL 8.0 开始,执⾏⼀条 SQL 查询语句,不会再⾛到查询缓存这个阶段了。
- 解析sql
- 词法分析:根据你输⼊的字符串识别出关键字出来
- 语法分析:根据词法分析的结果判断是否符合SQL语法,并构建SQL语法课
- 执行sql
- 预处理阶段:判断表和字段是否存在
- 优化阶段:将 SQL 查询语句的执⾏⽅案确定下来,⽐如在表⾥⾯有多个索引的时候,优化器会基于查询成本的考虑,来决定选择使⽤哪个索引, 或者在⼀个语句有多表关联(join)的时候,决定各个表的连接顺序。
- 执⾏阶段:MySQL通过分析器知道了你要做什么,通过优化器知道了该怎么做,于是就进⼊了执⾏器阶段,开始执 ⾏语句(执⾏语句时,⾸先会判断当前⽤户是否有执⾏权限)。
一条更新语句是如何工作的?
查询语句的流程,更新语句同样需要⾛⼀遍
- 执⾏语句前先连接数据库
- 数据库表有更新,跟表有关的查询缓存会失效,所以会清空之前的缓存结果
- 分析器进⾏词法和语法解析,优化器进⾏优化,执⾏器负责执⾏,然后更新。
但是更新流程涉及到了两个重要的⽇志模块: redo log(重做⽇志) 和 binlog(归档⽇志)
redo log 和 binlog 有什么不同? redo log 是 InnoDB 引擎特有的; binlog 是 MySQL 的 Server 层实现的,所有引擎都 可以使⽤。
- redo log 是物理⽇志,记录的是“在某个数据⻚上做了什么修改”; binlog 是逻辑⽇ 志,记录的是这个语句的原始逻辑,⽐如“给 ID=2 这⼀⾏的 c 字段加 1
- redo log 是循环写的,空间固定会⽤完; binlog 是可以追加写⼊的。“追加写”是指 binlog ⽂件写到⼀定⼤⼩后会切换到下⼀个,并不会覆盖以前的⽇志。
什么事最左匹配原则?
通过将多个字段组合成⼀个索引,该索引就被称为联合索引。
使⽤联合索引时,存在最左匹配原则,也就是按照最左优先的⽅式进⾏索引的匹配。
最左匹配原则要求查询条件中的列应该从索引的最左边的列开始,并且不能跳过中间的列。如果查询条件不按照索
引的顺序进⾏匹配,那么索引可能会失效。
举个例⼦:
- 如果查询条件为 WHERE column1 = 'value1' ,那么索引可以被有效使⽤。
- 如果查询条件为 WHERE column1 = 'value1' AND column2 = 'value2' ,同样索引可以被有效使⽤。
- 但如果查询条件为 WHERE column2 = 'value2' 或 WHERE column2 = 'value2' AND column3 = 'value3' ,则最左匹配原则不成⽴。
- 范围查询的影响:
- 当使用范围查询(例如 >, <)时,匹配过程会停止。
- 例如,如果你有一个索引 (column1, column2, column3), 在查询中:WHERE column1 = 'value1' AND column2 > 'value2':索引仍然可以用于 column1 和 column2,但无法进一步匹配 column3。
Redis
Redis RDB 过程中 COW 的具体工作原理
- RDB 生成快照过程
- Redis 执行
BGSAVE命令时,会 fork 一个子进程。子进程负责将数据写入磁盘,生成 RDB 文件。 - 子进程创建时,父进程和子进程共享同一块内存。由于子进程是通过 fork 方式创建的,子进程会继承父进程的内存数据,这样父进程和子进程都指向相同的物理内存页。
- Redis 执行
- COW 的作用
- 在 fork 之后,如果父进程需要对某块内存操作时,此时不能直接修改该内存,而是需要将修改的内存页复制一份(写时复制),这样父子进程不再共享相同内存,子进程仍然保留快照生成的旧数据,而父进程可以继续进行数据修改。
- 这样做的好处是子进程可以继续生成RDB快照,不会因为父进程修改而导致数据不一致。同时,内存的复制只有在需要修改的情况下才发生,这样可以大大节省资源。
Redis
单线程
Redis server 启动后,它的主要工作包括接收客户端请求、解析请求和进行数据读写等操作,是由单线程来执行的,这也是我们常说 Redis 是单线程程序的原因。
但是,Redis 还启动了 3 个线程来执行文件关闭、AOF 同步写和惰性删除等操作,从这个角度来说,Redis 又不能算单线程程序,它还是有多线程的。 https://learn.lianglianglee.com/专栏/Redis%20源码剖析与实战/12%20%20Redis真的是单线程吗?.md
多线程
Cluster
Gossip 协议
HTTP
tcp&udp
粘包和拆包
TCP协议是一种面向流的协议,在数据传输过程中,发送方和接收方之间可能会出现数据包粘连或拆散的现象,这就是所谓的"粘包"和"拆包"问题。这种问题主要发生在传输层,而UDP协议由于有消息保护边界,不会出现这种问题。 造成TCP粘包和拆包的主要原因包括:
- TCP是面向流的协议,没有消息保护边界,TCP传输的数据是以字节流的形式,没有明确的开始和结尾,所以TCP无法判断哪些字节属于同一个消息。
- 发送端发送的数据大于TCP发送缓冲区剩余空间,会导致拆包
- 发送的数据大于MSS(最大报文长度),TCP在传输前会进行拆包
- 发送的数据小于TCP发送缓冲区大小,TCP会将多次写入缓冲区的数据一次发送,导致粘包
- 接收端应用层没有及时读取接收缓冲区中的数据,也会导致粘包
- Nagle算法是为了提高网络利用率而设计的,它会将小数据包合并成一个大数据包发送。
影响点
- 降低网络传输效率 粘包会导致发送端发送的数据包过大,而拆包会导致发送端需要发送更多的数据包,这些都会增加网络传输的开销和延迟。
- 增加网络带宽的占用 粘包和拆包会导致发送端需要发送更多的数据包,从而增加了网络带宽的占用。
- 增加网络设备的处理负担 网络设备如路由器、交换机等需要对数据包进行拆分和重组,这会增加设备的处理负担。
- 增加应用程序的复杂性 开发人员需要额外编写代码来处理粘包和拆包问题,增加了应用程序的复杂性和开发难度,从而也会影响应用程序的性能。
解决TCP粘包和拆包的常见方法有:
- 发送端在每个数据包前添加包头,包含数据包长度信息,接收端据此分割数据包
- 发送端使用固定长度的数据包,接收端每次读取固定长度即可
- 在数据包之间添加特殊分隔符,接收端据此识别数据包边界
- 使用自定义的应用层协议,在协议层面解决粘包拆包问题
总之,TCP粘包和拆包是一个需要重点关注的网络编程问题,开发者需要采取有效措施来规避这些问题,确保应用程序的稳定性和可靠性。
RPC
原理

如何设计RPC协议
- 协议长度
- 序列化方式
- 协议头:协议标示、消息ID、消息类型
- 协议扩展字段
- payload
为什么需要序列化
网络传输的数据必须是二进制数据,但调用方请求的出入参数都是对象。
对象是不能直接在网络中传输的,所以我们需要提前把它转成可传输的二进制,并且要求转换算法是可逆的,这个过程我们一般叫做“序列化”。

常见序列化方式
- 语言原生序列化
- JSON
- Protobuf
- Thrift
选择序列化方式时,需要考虑性能、时间开销、空间开销、通用性、兼容性和安全性
RPC 网络通信方式
- 阻塞IO
- IO多路复用(更适合高并发的场景,可以用较少的进程(线程)处理较多的socket的IO请求)
- 非阻塞IO
- 异步IO(高版本Linux才有)
零拷贝
所谓的零拷贝,就是取消用户空间与内核空间之间的数据拷贝操作,应用进程每一次的读写操作,都可以通过一种方式,让应用进程向用户空间写入或者读取数据,就如同直接向内核空间写入或者读取数据一样,再通过DMA将内核中的数据拷贝到网卡,或将网卡中的数据copy到内核。
零拷贝有两种解决方式,分别是 mmap+write 方式和 sendfile 方式,mmap+write方式的核心原理就是通过虚拟内存来解决的

如何设计RPC框架
- 服务发现
- 健康检查
- 路由策略
- 异常重试
- 优雅重启、关闭
- 熔断限流
- 业务分组
- 安全体系(鉴权)
- 链路追踪
网络优化
网络请求优化
- 尽量减少不必要的网络IO
- 尽量合并请求
- 调用者机器和被调用者机器部署得近一些
- 内网调用优先于外网调用
接收过程优化
- 调整网卡 RingBuffer 的大小
- 多队列网卡 RSS 调优
- 硬中断合并
- 软中断 budget 调整
- 接收处理合并
发送过程优化
- 控制包的大小
- 减少内存分配
- 推迟分片
- 多队列网卡XPS调优
- 使用eBPF绕开协议栈的本地网络IO
内核进程优化
- 尽量少使用 recvfrom 等阻塞的网络调用
- 使用成熟的库
握手过程优化
- 充足的端口范围
- 客户端不使用 bind
- 打开 TCP FAST OPEN
- 充足的描述符上限
- 减少握手重试
- 请求频繁,短链接改为长链接
- TIME_WAIT 优化(建议1开启端⼝reuse 和recycle 第⼆个办法是限制TIME WAIT状态的连接的最⼤数量。)
锁
死锁
互斥锁
自旋锁
重入锁
- 虚拟内存
Linux 零拷贝技术原理
零拷贝技术旨在减少数据在用户空间和内核空间之间的拷贝次数,从而提高数据传输效率,降低 CPU 负载。在 Linux 中,主要有以下几种零拷贝技术:
- mmap + write
原理: 使用 mmap() 系统调用将文件映射到用户空间的虚拟内存地址,然后使用 write() 系统调用将数据直接写入到内核缓冲区,避免了数据从内核空间到用户空间的拷贝。 适用场景: 文件传输、网络传输等需要大量数据传输的场景。 缺点: 需要应用程序管理数据的缓存,增加了应用的复杂性。 可能导致文件内容的修改直接反映到磁盘上,需要谨慎使用。 2. sendfile
原理: 使用 sendfile() 系统调用将数据从一个文件描述符直接传输到另一个文件描述符,避免了数据在内核空间和用户空间之间的拷贝。 适用场景: 网络服务器发送静态文件等场景。 缺点: 只能用于文件到套接字的传输,不支持其他类型的文件操作。 需要内核支持 sendfile() 系统调用。 3. splice
原理: 使用 splice() 系统调用将数据在两个文件描述符之间移动,避免了数据在内核空间和用户空间之间的拷贝。 适用场景: 管道通信、网络传输等场景。 缺点: 需要内核支持 splice() 系统调用。 两个文件描述符必须是管道设备或套接字。 4. tee
原理: 使用 tee() 系统调用将数据从一个管道复制到另一个管道,避免了数据在内核空间和用户空间之间的拷贝。 适用场景: 需要将数据复制到多个目标的场景。 缺点: 需要内核支持 tee() 系统调用。 两个文件描述符必须是管道设备。 5. sendfile + DMA gather copy
原理: 结合 sendfile() 和 DMA gather copy 技术,将多个分散的数据块直接传输到网络设备,避免了数据在内核空间的拷贝。 适用场景: 高性能网络服务器发送大量小文件等场景。 缺点: 需要硬件支持 DMA gather copy。 需要内核支持相关特性。 总结:
零拷贝技术可以显著提高数据传输效率,降低 CPU 负载,但不同的技术有不同的适用场景和限制。选择合适的零拷贝技术需要根据具体的应用场景和需求进行评估。
分布式理论
CAP 理论,为什么不能同时满⾜
CAP 理论是分布式系统设计中的三个基本属性,它们分别是⼀致性(Consistency)、可⽤性(Availability)、和 分区容错性(Partition Tolerance)。CAP 理论由计算机科学家 Eric Brewer 在2000年提出。
- 一致性:一致性要求所有节点数据要一致。如果一个节点上修改了数据,那么其他节点也应该立即看到修改变更
- 可用性:可用性要求系统能对用户的请求作出响应,即便出现节点故障的情况下仍然保持可用。
- 分区容错性:系统面对网络分区的情况下仍然能工作,即节点之间出现网络故障无法通信时,仍然要保持一致性和可用性
- 一致性和分区容错性(牺牲可用性)CP: 分布式数据库\金融系统: 例如银行账户系统,需要确保每次交易都是一致的,即所有用户看到的账户余额必须是最新的。这种系统在网络分区时可能会选择暂时停止交易操作,以保持一致性。
- 可用性和分区容错性(牺牲一致性)AP: 社交网络和网络购物:例如微博或Facebook等社交媒体应用,需要确保用户始终能够发布帖子或查看内容,即使在网络分区的情况下。数据一致性可以在后台通过异步同步的方式来解决。 电商平台需要确保用户能够浏览商品和进行购买,即使在部分服务器不可用时。数据一致性的问题可以通过后台的补偿机制来处理。
- 一致性和可用性(牺牲分区容错性)CA: 内部企业系统和单节点数据库 (系统不具备分区容错性,网络或节点出现故障可能导致系统不可用。)
BASE 理论
BASE 理论,它是 CAP 理论的延伸。BASE 是 Basically Available(基本可用)、Soft State(软状态)和 Eventually Consistent(最终一致性)三个单词的简写,作用是保证系统的可用性,然后通过最终一致性来代替强一致性,它是目前分布式系统设计中最具指导意义的经验总结。
在做分库分表时,基于 Hash 取模和一致性 Hash 的数据分片是如何实现的?
基于 Hash 取模的数据分片
- 选择分片键。例如:用户ID,订单ID
- 计数分片键hash值。常用哈希算法MD5,SHA-1
- 取模运算。将 Hash 值对数据库或表的数量进行取模运算,结果即为数据存储的目标库或表的索引
一致性 Hash 的数据分片
- 构建一致性hash环。将整个hash空间构建成一个0-2的32次方-1大小的环。将数据库、表映射到环上的虚拟节点
- 计算分片的键hash值。对分片键hash计算,得到其在环上的位置
- 寻找最近的节点。从计算的分片hash值位置开始,沿顺时针方向查找最近的虚拟节点,该节点对应的数据存储库/表
- 数据存储 优点:当节点增加/减少是,仅需要重分布少量的数据。数据分布相对均匀,避免数据倾斜问题。 缺点:实现起来复杂。虚拟节点管理,数据迁移,平衡性等。
强一致性算法和最终一致性算法(共识算法)
强一致性保证了在任何时候,所有节点都能看到数据的最新状态。也就是说,写入操作成功后,任何读取操作都能返回最新的数据。这种一致性通常通过以下数据共识算法实现:
- Paxos:Paxos 是一种经典的分布式共识算法,它通过一系列的消息传递步骤来保证强一致性。在 Paxos 中,存在三个角色:提议者(Proposer)、接受者(Acceptor)和学习者(Learner)。提议者提出值,接受者决定是否接受值,学习者得到最终的决定值。Paxos 保证在大多数接受者同意的情况下,提议的值会被确定,从而保证强一致性。
- Raft:Raft 是一种更易理解的共识算法,也是 Paxos 的替代品。它通过选举一个领导者来简化共识过程。所有写操作都通过领导者处理,领导者将更改复制到其他节点上,并等待大多数节点确认。这种机制确保了系统中的每个节点都达成一致,从而实现强一致性。
- Zookeeper’s ZAB (Zookeeper Atomic Broadcast):ZAB 是 Zookeeper 分布式协调服务使用的共识协议,它类似于 Paxos 和 Raft。ZAB 保证在领导者发生变更时,仍然能够保持数据的一致性和顺序性,从而提供强一致性。
最终一致性允许系统中的所有节点在没有立即同步的情况下,最终达到一致的状态。虽然在短时间内不同节点可能看到不同的数据,但随着时间的推移,所有节点都会收敛到一致的状态。这通常通过以下策略实现:
- Gossip Protocol:Gossip 协议是一种去中心化的传播方式,每个节点会周期性地与其他节点交换信息,从而逐渐将数据传播到整个系统中。随着时间的推移,所有节点最终会达到一致的状态。Cassandra 和 DynamoDB 等系统采用了这种协议来实现最终一致性。
- Vector Clocks:矢量时钟用于跟踪系统中不同节点的操作顺序,并帮助检测冲突。矢量时钟记录每个节点上数据的版本号,并在读取时将这些版本返回给客户端。如果存在冲突,系统可以通过应用某种冲突解决策略来实现一致性。
- Anti-Entropy Mechanisms:反熵机制通过定期同步数据来修复分布式系统中的数据不一致性。例如,节点之间可以定期交换哈希值来检测不一致,并修复差异。
限流
sentinel
缓存一致性

分布式锁
- Redis
- Etcd
- mysql主键
分布式锁过期如何处理
- 设置合理的过期时间
- 自动续期
- watchDog 机制
Redisson 底层实现
数组
41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
解释:最小的正数 1 没有出现。
解题思路:
- 第一次遍历数组,将每个正整数放置在正确的位置上
- 第二次遍历数组,找到缺失的最小正整数
- 如果数组中的所有正整数都在正确的位置上,则返回数组长度加一
func firstMissingPositive(nums []int) int {
n := len(nums)
for i := 0; i < n; i++ {
// 假设nums[i] =k, k应该放置索引k-1位置,因此就有 nums[i]=nums[nums[i]-1]
for nums[i] > 0 && nums[i] <= n; nums[nums[i]-1] != nums[i] {
nums[i], nums[nums[i]-1] = nums[nums[i]-1], nums[i]
}
}
// 第二次遍历,找出缺少的最小正整数
for i := 0; i < n; i++ {
if nums[i] != i+1{
return i+1
}
}
}
004.寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
Example:
Input: nums1 = [1, 3], nums2 = [2]
Output: 1.5
解题思路:
- 首先,确保第一个数组长度小于第二个数组,如果不是就交换,确保第一个数组时较短的那个
- 然后,用二分法在第一个数组选择一个分割点,将数组分割成两部分,使得左半部分的元素小于有半部分的元素
- 继而,用同样方法把第二个数组分割,使得第一个数组和第二个数组的左半部分的元素个数之和等于右半部分的元素个数之和。
- 当我们找到这样的分割点时,中位数可以通过以下步骤计算得出: 如果两个数组的元素总数是奇数,中位数就是分割点左边部分的最大值。 如果两个数组的元素总数是偶数,中位数就是分割点左边部分的最大值和右边部分的最小值的平均值。
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
if len(nums1) > len(nums2) {
nums1, nums2 = nums2, nums1
}
m, n := len(nums1), len(nums2)
left, right := 0, m
median1, median2 := 0, 0
for left <= right {
// 数组1 的分割点
partition1 := (left + right) / 2
// 保证两个数组左半部分和右半部分元素个数和相等,那么第二个数组的分割点就是:
// 两个数组左半边部分元素个数(m+n+1)/2 - 第一个数组的分割点
partition2 := (m+n+1)/2 - partition1
maxLeft1, maxLeft2 := math.MinInt64, math.MinInt64
if partition1 > 0 {
maxLeft1 = nums1[partition1-1]
}
if partition2 > 0 {
maxLeft2 = nums2[partition2-1]
}
minRight1, minRight2 := math.MaxInt64, math.MaxInt64
if partition1 < m {
minRight1 = nums1[partition1]
}
if partition2 < n {
minRight2 = nums2[partition2]
}
// 如果数组1 左半部分最大值小于等于 数组2右半部分最小值
// 如果数组1 左半部分最小值大于等于 数组2左半部分最大值
// 说明分割点找对了
if maxLeft1 <= minRight2 && maxLeft2 <= minRight1 {
// 总数组元素个数是偶数时,我们取左半部分的最大值和右半部分的最小值,并计算它们的平均值作为中位数
if (m+n)%2 == 0 {
median1 = max(maxLeft1, maxLeft2)
median2 = min(minRight1, minRight2)
return float64(median1+median2) / 2
} else {
// 总数组元素个数是奇数时,我们直接取左半部分的最大值作为中位数。
median1 = max(maxLeft1, maxLeft2)
return float64(median1)
}
// 如果数组1左边最大值大于数组2右边最小值,说明两个数组按顺序排序的话,应该是 nums2...nums1
// 所以中位数应该在 nums1 分割点左边
} else if maxLeft1 > minRight2 {
right = partition1 - 1
} else {
// 如果数组1左边最大值小于数组2右边最小值,说明两个数组按顺序排序的话,应该是 nums1...nums2
// 所以中位数应该在 nums1 分割点右边
left = partition1 + 1
}
}
return -1.0
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
47.全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示: 1 <= nums.length <= 8 -10 <= nums[i] <= 10
解题思路:
func permuteUnique(nums []int) [][]int {
var result [][]int
var backtrack func(path []int, remaining []int)
backtrack = func(path, remaining []int) {
if len(path) == len(nums) {
temp := make([]int, len(path))
copy(temp, path)
result = append(result, temp)
return
}
// 判断去重
for i := 0; i < len(remaining); i++ {
// 去重
if i > 0 && remaining[i-1] == remaining[i] {
continue
}
path = append(path, remaining[i])
nextremaining := make([]int, len(remaining)-1)
copy(nextremaining[:i], remaining[:i])
copy(nextremaining[i:], remaining[i+1:])
backtrack(path, nextremaining)
path = path[:len(path)-1]
}
}
// 排序
sort.Ints(nums)
backtrack(nil, nums)
return result
}
39.组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
解题思路
- 对
candidates排序 - 递归函数,combination 当前组合、remaining 剩余的目标值,start 游标
- remaining == 0 找到有效组合
- remaining < 0 不符合,直接返回
- 遍历
candidates数组,注意start可以重复选择
func combinationSum(candidates []int, target int) [][]int {
// 排序
sort.Ints(candidates)
var results [][]int
var backtrack func(combinations []int, remaining int, index int)
backtrack = func(combinations []int, remaining int, index int) {
if remaining == 0 {
// 找到符合组合
tmp := make([]int, len(combinations))
copy(tmp, combinations)
results = append(results, tmp)
return
}
if remaining < 0 {
// 不符合直接返回
return
}
// 遍历候选数组
for i := index; i < len(candidates); i++ {
combinations = append(combinations, candidates[i])
backtrack(combinations, remaining-candidates[i], i)
combinations = combinations[:len(combinations)-1]
}
}
backtrack([]int{}, target, 0)
return results
}
旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1: 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2: 输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示: n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000
解题思路
原地旋转图像,我们可以采取以下步骤:
- 转置矩阵: 将矩阵沿主对角线翻转,即 matrix[i][j] 与 matrix[j][i] 交换位置。
- 翻转每一行: 将转置后的矩阵的每一行进行翻转,即可得到顺时针旋转90度的结果。
func rotate(matrix [][]int) {
n := len(matrix)
// 转置矩阵
for i := 0; i < n; i++ {
for j := i; j < n; j++ {
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
}
}
// 逆序每行
for i := 0; i < n; i++ {
for j := 0; j < n / 2; j++ {
matrix[i][j], matrix[i][n-j-1] = matrix[i][n-j-1], matrix[i][j]
}
}
}
169.多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示:
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
解题思路:
- 哈希表:时间复杂度 O(n),空间复杂度 O(n)
- 排序: 时间复杂度 O(nlogn),空间复杂度 O(1)
- Boyer-Moore 投票算法(最优解)
// 哈希表:时间复杂度 O(n),空间复杂度 O(n)
func majorityElement(nums []int) int {
m := len(nums) / 2
var mp = make(map[int]int)
for _, num := range nums {
mp[num] += 1
if mp[num] > m {
return num
}
}
return 0
}
// 排序: 时间复杂度 O(nlogn),空间复杂度 O(1)
func majorityElement1(nums []int) int {
sort.Ints(nums)
return nums[len(nums)/2]
}
/*
Boyer-Moore 投票算法(最优解)
核心思想:维护一个候选元素和计数器
- 遇到相同元素计数加1,不同元素计数减1
- 计数为0时更换候选元素
时间复杂度 O(n),空间复杂度 O(1)
*/
func majorityElement2(nums []int) int {
// 候选元素
candidate := nums[0]
// 计数器
counter := 1
// boyer-moore 投票
for i := 1; i < len(nums); i++ {
// 如果计数为0, 说明前面的元素都不同/元素相同, 更换候选元素
if counter == 0 {
candidate = nums[i]
}
if nums[i] == candidate {
counter++
} else {
counter--
}
}
return candidate
}
179.最大数
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2]
输出:"210"
示例 2:
输入:nums = [3,30,34,5,9]
输出:"9534330"
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 109
解题思路:
- 这本质是一个排序问题,关键在于定义正确的比较规则
- 对于两个数字 a 和 b,我们需要比较 "ab" 和 "ba" 的大小:
- 如果 "ab" > "ba",则 a 应该排在 b 前面
- 如果 "ab" < "ba",则 b 应该排在 a 前面
- 使用自定义排序规则对数组进行排序
- 特殊处理:如果排序后第一个数字是0,则结果就是"0"
func largestNumber(nums []int) string {
if len(nums) == 0 {
return ""
}
var strNums = make([]string, len(nums))
for i, num := range nums {
strNums[i] = strconv.Itoa(num)
}
// 自定义排序
sort.Slice(strNums, func(i, j int) bool {
return strNums[i]+strNums[j] > strNums[j] + strNums[i]
})
// 特殊情况
if strNums[0] == "0" {
return "0"
}
return strings.Join(strNums, "")
}
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
解题思路:
- 将所有元素添加到集合中: 这样可以在 O(1) 时间内检查某个元素是否存在。
- 遍历集合中的每个元素: 如果当前元素的前驱元素(即 num - 1)不存在于集合中,则说明当前元素是一个连续序列的起点。 接着,顺序查找当前元素的后续元素,计算当前序列的长度。
- 记录最长的序列长度: 在遍历过程中,保持记录最大序列长度。
func longestConsecutive(nums []int) int {
var numSet = make(map[int]bool)
for _, num := range nums {
numSet[num] = true
}
var result int
// 检查 num-1 是否存在集合,即可判断是否是序列起点
for num := range numSet {
if !numSet[num-1] {
currNum := num
currSeq := 1
for numSet[currNum+1] {
currNum++
currSeq++
}
if currSeq > result {
result = currSeq
}
}
}
return result
}
206.反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
解题思路:
创建一个前节点,依次反转
func reverseList(head *ListNode) *ListNode {
var prev *ListNode
var curr = head
for curr != nil {
next := curr.Next
curr.Next = prev
prev = curr
curr = next
}
return prev
}
2.两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
Example:
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807
Constraints:
- The number of nodes in each linked list is in the range [1, 100].
- 0 <= Node.val <= 9
- It is guaranteed that the list represents a non-negative integer.
解题思路:
- Create a new linked list to store the sum.
- Initialize a carry variable to 0.
- Iterate through the input lists, adding the corresponding digits and carrying over any overflow.
- For each iteration:
- Add the current digits of the two lists, along with the carry.
- Calculate the new carry and the digit to add to the sum list.
- Add the new digit to the sum list.
- If there is a remaining carry, add it to the sum list.
- Return the sum list.
Code:
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
dummy := &ListNode{Val: 0, Next: nil}
curr := dummy
carry := 0
for l1 != nil || l2 != nil || carry != 0 {
sum := carry
if l1 != nil {
sum += l1.Val
l1 = l1.Next
}
if l2 != nil {
sum += l2.Val
l2 = l2.Next
}
carry = sum / 10
curr.Next = &ListNode{Val: sum % 10}
curr = curr.Next
}
return dummy.Next
}
19.删除链表的倒数第N个节点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1 输出:[]
示例 3:
输入:head = [1,2], n = 1 输出:[1]
提示:
链表中结点的数目为 sz 1 <= sz <= 30 0 <= Node.val <= 100 1 <= n <= sz
解题思路:
这个问题可以用双指针技巧来解决。
我们可以使用两个指针,一个快指针 fast 和一个慢指针 slow,它们都指向链表的头节点。
- 首先,我们将 fast 指针向前移动 n 个节点。
- 然后,同时移动 fast 和 slow 指针,直到 fast 指针到达链表末尾。
- 此时,slow 指针将指向倒数第 n 个节点的前一个节点。我们只需要将 slow 指针的 next 指针指向 slow.next.next 即可删除倒数第 n 个节点。 特殊情况处理:
- 如果链表只有一个节点,而 n = 1,我们需要返回空链表。
- 如果 n 等于链表的长度,我们需要删除头节点。
func removeNthFromEnd(head *ListNode, n int) *ListNode {
dummy := &ListNode{
Val: 0,
Next: head,
}
fast, slow := dummy, dummy
// 注意:n+1步,前面引入了哑结点
for i := 0; i <= n; i++ {
fast = fast.Next
}
for fast != nil {
fast = fast.Next
slow = slow.Next
}
slow.Next = slow.Next.Next
return dummy.Next
}
21.合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
两个链表的节点数目范围是 [0, 50] -100 <= Node.val <= 100 l1 和 l2 均按 非递减顺序 排列
Related Topics 递归 链表 👍 3195 👎 0
解题思路:
- 如果 l1 或 l2 为空,直接返回另一个非空链表。
- 比较头节点: 比较 l1 和 l2 的头节点值,将较小值的节点作为新链表的头节点。
- 递归调用: 将较小值节点的 next 指针指向 l1 和 l2 剩余部分合并后的链表(通过递归调用实现)。
- 返回新链表的头节点。
func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
var dummy = &ListNode{}
current := dummy
for list1 != nil && list2 != nil {
if list1.Val < list2.Val {
current.Next = list1
// 往后移动list1
list1 = list1.Next
} else {
current.Next = list2
// 往后移动list2
list2 = list2.Next
}
current = current.Next
}
// 分别把 list1 / list2 剩余的补到后面
if list1 != nil {
current.Next = list1
}
if list2 != nil {
current.Next = list2
}
return dummy.Next
}
234.回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为 回文链表 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:head = [1,2,2,1]
输出:true
示例 2:
输入:head = [1,2]
输出:false
解题思路
- 首先用快慢指针,找到中间节点
- 以中间节点为头节点的链表,反转
- 对比两链表是否相等
- 注意链表数为奇数的情况
func isPalindrome(head *ListNode) bool {
var fast, slow = head, head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
slow = slow.Next
}
rev := reverse(slow)
for rev != nil {
if head.Val != rev.Val { // 注意比较的是值
return false
}
rev = rev.Next
head = head.Next
}
return true
}
func reverse(head *ListNode) *ListNode{
var prev *ListNode
var curr = head
for curr != nil {
temp := curr.Next // 注意
curr.Next = prev
prev = curr
curr = temp // 注意
}
return prev // 注意
}
LCR 140. 训练计划 II
给定一个头节点为 head 的链表用于记录一系列核心肌群训练项目编号,请查找并返回倒数第 cnt 个训练项目编号。
示例 1:
输入:head = [2,4,7,8], cnt = 1
输出:8
解题思路
- 初始化: 前指针 former 、后指针 latter ,双指针都指向头节点 head 。
- 构建双指针距离: 前指针 former 先向前走 cnt 步(结束后,双指针 former 和 latter 间相距 cnt 步)。
- 双指针共同移动: 循环中,双指针 former 和 latter 每轮都向前走一步,直至 former 走过链表 尾节点 时跳出(跳出后,latter 与尾节点距离为 cnt−1cnt-1cnt−1,即 latter 指向倒数第 cnt 个节点)。
func trainingPlan(head *ListNode, cnt int) *ListNode {
var fast, slow = head, head
for i := 0; i < cnt; i++ {
fast = fast.Next
}
for fast.Next != nil {
fast = fast.Next
slow = slow.Next
}
return slow.Next
}
83. 删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例1:
输入:head = [1,1,2]
输出:[1,2]
示例2:
输入:head = [1,1,2,3,3]
输出:[1,2,3]
解题思路:
- 由于链表已经排序,相同的节点一定相邻
- 比较相邻节点,如果相同跳到下一个节点
- 否则更新当前节点
- 注意循环条件判断
func deleteDuplicates(head *ListNode) *ListNode {
curr := head
// 注意循环条件
for curr != nil && curr.Next != nil {
next := curr.Next
if curr.Val == next.Val {
curr.Next = next.Next
}else {
curr = next // 注意,更新curr 不是 curr.Next
}
}
return head
}
电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = "" 输出:[]
示例 3:
输入:digits = "2" 输出:["a","b","c"]
提示:
0 <= digits.length <= 4 digits[i] 是范围 ['2', '9'] 的一个数字。
Related Topics 哈希表 字符串 回溯 👍 2805 👎 0
解题思路:
- 构建映射表: 首先,我们需要建立一个数字到字母的映射表,例如 2 对应 abc,3 对应 def 等等。
- 定义回溯函数: 该函数接受当前组合字符串和剩余数字作为参数。
- 递归搜索:
- 如果没有剩余数字,则将当前组合添加到结果列表中并返回。
- 否则,遍历当前数字对应的字母:
- 将当前字母添加到组合字符串中。
- 对剩余数字进行递归调用。
- 从组合字符串中删除当前字母(回溯)
func letterCombinations(digits string) []string {
// 建立数字到字母的映射关系
mapping := map[byte]string{
'2': "abc",
'3': "def",
'4': "ghi",
'5': "jkl",
'6': "mno",
'7': "pqrs",
'8': "tuv",
'9': "wxyz",
}
var result = []string{}
var backtrack func(res string, nextDigitStr string)
backtrack = func(res string, nextDigitStr string) {
if len(nextDigitStr) == 0 {
result = append(result, res)
return
}
letters := mapping[nextDigitStr[0]]
for _, let := range letters {
backtrack(res+string(let), nextDigitStr[1:])
}
}
backtrack("", digits)
return result
}
括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1 输出:["()"]
提示:
1 <= n <= 8
解题思路:
-
定义递归函数 generate(left, right, path, result):
- left: 剩余左括号数量
- right: 剩余右括号数量
- path: 当前生成的括号字符串
- result: 最终结果列表
-
结束条件:
当 left 和 right 都为 0 时,说明生成了一个有效的括号组合,将其添加到 result 中。 递归步骤: -
如果还有剩余左括号 (left > 0),则添加一个左括号到 path,并递归调用 generate(left-1, right, path+"(", result)。
-
如果右括号数量大于左括号数量 (right > left),则添加一个右括号到 path,并递归调用 generate(left, right-1, path+")", result)。
func generateParenthesis(n int) []string {
var result []string
var backtrack func(left, right int, path string, res *[]string)
backtrack = func(left, right int, path string, res *[]string) {
if left == 0 && right == 0 {
*res = append(*res, path)
return
}
// 左括号有剩余
if left > 0 {
backtrack(left-1, right, path+"(", res)
}
if right > left {
backtrack(left, right-1, path+")", res)
}
}
backtrack(n, n, "", &result)
return result
}
/*
思路:回溯法
*/
func generateParenthesis2(n int) []string {
var result []string
backtrack("", 0, 0, n, &result)
return result
}
func backtrack(path string, left, right, n int, result *[]string) {
// 终止条件,当path长度达2*n
if len(path) == 2*n {
*result = append(*result, path)
return
}
// 先放左括号
if left < n {
backtrack(path+"(", left+1, right, n, result)
}
if right < left {
backtrack(path+")", left, right+1, n, result)
}
}
112.路径总和
递归
func hasPathSum(root *TreeNode, targetSum int) bool {
if root == nil {
return false
}
targetSum -= root.Val
if root.Left == nil && root.Right == nil {
return targetSum == 0
}
return hasPathSum(root.Left, targetSum) || hasPathSum(root.Right, targetSum)
}
栈方法
func hasPathSum(root *TreeNode, targetSum int) bool {
if root == nil {
return false
}
stack := []struct {
node *TreeNode
sum int
}{{root, targetSum}}
for len(stack) > 0 {
current := stack[len(stack)-1]
stack = stack[:len(stack)-1]
node, sum := current.node, current.sum
sum -= node.Val
if node.Left == nil && node.Right == nil && sum == 0 {
return true
}
if node.Right != nil {
stack = append(stack, struct {
node *TreeNode
sum int
}{node.Right, sum})
}
if node.Left != nil {
stack = append(stack, struct {
node *TreeNode
sum int
}{node.Left, sum})
}
}
return false
}
LCR 140. 训练计划 II
给定一个头节点为 head 的链表用于记录一系列核心肌群训练项目编号,请查找并返回倒数第 cnt 个训练项目编号。
示例 1:
输入:head = [2,4,7,8], cnt = 1
输出:8
解题思路
- 初始化: 前指针 former 、后指针 latter ,双指针都指向头节点 head 。
- 构建双指针距离: 前指针 former 先向前走 cnt 步(结束后,双指针 former 和 latter 间相距 cnt 步)。
- 双指针共同移动: 循环中,双指针 former 和 latter 每轮都向前走一步,直至 former 走过链表 尾节点 时跳出(跳出后,latter 与尾节点距离为 cnt−1cnt-1cnt−1,即 latter 指向倒数第 cnt 个节点)。
func trainingPlan(head *ListNode, cnt int) *ListNode {
var fast, slow = head, head
for i := 0; i < cnt; i++ {
fast = fast.Next
}
for fast.Next != nil {
fast = fast.Next
slow = slow.Next
}
return slow.Next
}
11.盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
n == height.length 2 <= n <= 10⁵ 0 <= height[i] <= 10⁴
Related Topics 贪心 数组 双指针 👍 4953 👎 0
func maxArea(height []int) int {
var left, right = 0, len(height) - 1
var maxArea = 0
for left < right {
// 面积=最短的高度 * 宽度
area := min(height[left], height[right]) * (right - left)
if area > maxArea {
maxArea = area
}
// 要获得最多面积,移动短的一端
if height[left] < height[right] {
left++
} else {
right--
}
}
return maxArea
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
0043.字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1: 输入: num1 = "2", num2 = "3" 输出: "6"
示例 2: 输入: num1 = "123", num2 = "456" 输出: "56088"
提示: 1 <= num1.length, num2.length <= 200 num1 和 num2 只能由数字组成。 num1 和 num2 都不包含任何前导零,除了数字0本身。
解题思路
- 反转字符串
- 逐位相乘,进位相加,求余
- 去除前置零
- 转为字符串
func multiply(num1 string, num2 string) string {
// 反转字符串
num1 = reverse(num1)
num2 = reverse(num2)
var products = make([]int, len(num1)+len(num2))
// 逐位相乘, 进位相加,求余
for i := 0; i < len(num1); i++ {
for j := 0; j < len(num2); j++ {
products[i+j] += int(num1[i]-'0') * int(num2[j]-'0')
// 处理进位
products[i+j+1] += products[i+j] / 10
products[i+j] = products[i+j] % 10
}
}
// 去掉前置0
for len(products) > 1 && products[len(products)-1] == 0 {
products = products[:len(products)-1]
}
// 转为字符串
var result string
for i := len(products) - 1; i >= 0; i-- {
result += fmt.Sprint(products[i])
}
return result
}
func reverse(str string) string {
var result = []rune(str)
var left, right = 0, len(result) - 1
for left < right {
result[left], result[right] = result[right], result[left]
left++
right--
}
return string(result)
}
0151.反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
输入:s = "the sky is blue" 输出:"blue is sky the"
输入:s = " hello world " 输出:"world hello"
解题思路:
- 去除多余空格
- 先把字符串中的所有单词分割成数组。
- 然后反转数组中的元素顺序。
- 最后把反转后的数组重新拼接成字符串,并在每个单词之间加一个空格。
func reverseWords(s string) string {
// 1. 去除多余空格
s = spaceTrim(s)
// 转slice
arr := strings.Split(s, " ")
var left, right = 0, len(arr) - 1
for left < right {
arr[left], arr[right] = arr[right], arr[left]
left++
right--
}
return strings.Join(arr, " ")
}
func spaceTrim(s string) string {
// 去除前导空格
for len(s) > 1 && s[0] == ' ' {
s = s[1:]
}
// 去除尾随空格
for len(s) > 0 && s[len(s)-1] == ' ' {
s = s[:len(s)-1]
}
// 去除中间多余空格
i := 1
for i < len(s)-1 {
if s[i] == ' ' && s[i+1] == ' ' {
s = s[:i] + s[i+1:]
} else {
i++
}
}
return s
}
0032.最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1: 输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()"
示例 2: 输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()"
示例 3: 输入:s = "" 输出:0
提示: 0 <= s.length <= 3 * 10⁴ s[i] 为 '(' 或 ')'
解题思路:
- 维护一个栈,遇到( 入栈,遇到 ) 弹出栈顶元素
- 栈为空,当前右括号为新的起始点(引入-1为辅助栈元素)
- 更新最长括号长度
func longestValidParentheses(s string) int {
// 假设我们的字符串是 "()",这时如果没有初始的-1在栈中,那么在遇到第一个右括号时,栈为空,无法确定有效括号的起始点。因此,我们将-1作为初始值放入栈中,当遇到右括号时,就可以直接使用它作为起始点。
stack := []int{-1} // 栈,初始化时压入-1作为辅助计算长度
maxLength := 0
for i, char := range s {
if char == '(' { // 左括号
stack = append(stack, i)
} else { // 右括号
stack = stack[:len(stack)-1] // 弹出栈顶元素
if len(stack) == 0 { // 栈为空,当前右括号为新的起始点
stack = append(stack, i)
} else { // 更新最长有效括号长度
length := i - stack[len(stack)-1]
if length > maxLength {
maxLength = length
}
}
}
}
return maxLength
}
6.Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N A P L S I I G Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3 输出:"PAHNAPLSIIGYIR"
示例 2:
输入:s = "PAYPALISHIRING", numRows = 4 输出:"PINALSIGYAHRPI" 解释: P I N A L S I G Y A H R P I
示例 3:
输入:s = "A", numRows = 1 输出:"A"
提示:
1 <= s.length <= 1000 s 由英文字母(小写和大写)、',' 和 '.' 组成 1 <= numRows <= 1000
解题思路:
- 观察规律: 仔细观察 Z 字形排列规律,你会发现字符串在 Z 字形路径上移动,每次移动都是先向下,再斜向上。
- 模拟路径: 我们可以使用 numRows 个字符串数组来存储每一行的字符。遍历字符串 s,根据当前行数和移动方向,将字符添加到对应行的数组中。
- 拼接结果: 最后,将所有行的字符串数组依次拼接起来,即可得到最终的 Z 字形变换后的字符串。
func convert(s string, numRows int) string {
// 长度为1和numRows小于原字符串长度,无需变换
if numRows == 1 || len(s) <= numRows {
return s
}
// 定义 numRows 长度一维数组用于保存变换的字符子串
rows := make([]string, numRows)
// 一维数组元素位置
var index = 0
// step 用于区别遍历的方向
var step = 1
for i := 0; i < len(s); i++ {
rows[index] += string(s[i])
// 如果到达数组首位,也改变遍历方向,反方向
if index == 0 {
step = 1
}
// 如果到达数组末位,改变遍历方向
if index == numRows-1 {
step = -1
}
index += step
}
var ans string
for _, row := range rows {
ans += row
}
return ans
}
字符串转整数
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。 将前面步骤读入的这些数字转换为整数(即,"123" -> 123, "0032" -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。 如果整数数超过 32 位有符号整数范围 [−2³¹, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −2³¹ 的整数应该被固 定为 −2³¹ ,大于 231 − 1 的整数应该被固定为 231 − 1 。 返回整数作为最终结果。
注意:
本题中的空白字符只包括空格字符 ' ' 。 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
输入:s = "42" 输出:42 解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。 第 1 步:"42"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"42"(读入 "42") ^ 解析得到整数 42 。 由于 "42" 在范围 [-2³¹, 2³¹ - 1] 内,最终结果为 42 。
示例 2:
输入:s = " -42" 输出:-42 解释: 第 1 步:" -42"(读入前导空格,但忽视掉) ^ 第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42"(读入 "42") ^ 解析得到整数 -42 。 由于 "-42" 在范围 [-2³¹, 2³¹ - 1] 内,最终结果为 -42 。
示例 3:
输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-2³¹, 2³¹ - 1] 内,最终结果为 4193 。
提示:
0 <= s.length <= 200 s 由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-' 和 '.' 组成
Related Topics 字符串 👍 1806 👎 0
思路:
- 去掉空格
- 判断正负
- 遍历字符串,非法字符直接退出。数字字符*10累加
- 判断溢出
func myAtoi(s string) int {
// 1. 去掉空格
s = strings.TrimSpace(s)
if s == "" {
return 0
}
// 2. 判断正负
var sign = 1
if s[0] == '-' || s[0] == '+' {
if s[0] == '-' {
sign = -1
}
s = s[1:]
}
result := 0
for _, ch := range s {
// 非数字字符
if ch < '0' || ch > '9' {
break
}
result = result*10 + int(ch-'0')
if result > math.MaxInt32 {
if sign == -1 {
return math.MinInt32
}
return math.MaxInt32
}
}
return result * sign
}
正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符 '*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = "." 输出:true 解释:"." 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 20 1 <= p.length <= 20 s 只包含从 a-z 的小写字母。 p 只包含从 a-z 的小写字母,以及字符 . 和 *。 保证每次出现字符 * 时,前面都匹配到有效的字符
Related Topics 递归 字符串 动态规划 👍 3886 👎 0
func isMatch(s string, p string) bool {
m, n := len(s), len(p)
// 创建 m+1 和 n+1 长度,是因为我们需要考虑空字符串的情况以及边界条件。
// 通过在 dp 数组的第一行和第一列中预留出额外的位置,我们可以方便地处理空字符串的情况
// 将空字符串和正则表达式的匹配情况表示在 dp[0][0]、dp[0][j] 和 dp[i][0] 中。
// 二维数组,dp[i][j] 表示 s 前 i 个字符和 p 前 j 是否能匹配
dp := make([][]bool, m+1)
for i := 0; i <= m; i++ {
dp[i] = make([]bool, n+1)
}
// dp[0][0] 空字符串和空正则表达式是匹配的
dp[0][0] = true
// dp[0][j] 处理边界情况:当s为空字符串时,只有p的偶数位置为*才能匹配
for j := 2; j <= n; j += 2 {
if p[j-1] == '*' && dp[0][j-2] {
dp[0][j] = true
}
}
// dp[i][0] 表示 p 为空,因此所有都是 false 不需要处理,默认 false
// dp递推
// '.' 匹配任意单个字符
// '*' 匹配零个或多个前面的那一个元素
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
// 如果 s 的第 i 个字符和 p 的第 j 个字符相等,或者 p 的第 j 个字符等于 '.' 都可以匹配上
if s[i-1] == p[j-1] || p[j-1] == '.' {
dp[i][j] = dp[i-1][j-1]
} else if p[j-1] == '*' {
// 如果p的第j个字符为'*',有两种情况:
// 1. 匹配0个前导字符,即将p的前两个字符(x*)忽略掉,dp[i][j-2]
// 2. 匹配1个或多个前导字符,即s的第i个字符和p的前一个字符相等,且dp[i-1][j]为真
dp[i][j] = dp[i][j-2] || (s[i-1] == p[j-2] /* 匹配1个*/ || p[j-2] == '.' /* 匹配多个*/) && dp[i-1][j]
}
}
}
return dp[m][n]
}
14.最长公共前缀
解题思路:
- 初始化: 将第一个字符串假设为公共前缀。
- 遍历其他字符串: 依次检查每个字符串是否具有相同的前缀。如果发现一个字符串在某个位置的字符与公共前缀不同或公共前缀的长度超过该字符串的长度,则截断公共前缀到该位置的字符。
- 返回结果: 在所有字符串都比较完之后,剩下的公共前缀就是答案。
func longestCommonPrefix(strs []string) string {
if len(strs) == 0 {
return ""
}
prefix := getMinLenEle(strs)
var ans []byte
for i := range prefix {
for _, s := range strs[1:] {
if s[i] != prefix[i] {
return string(ans)
}
}
ans = append(ans, prefix[i])
}
return string(ans)
}
func getMinLenEle(strs []string) string {
n := len(strs[0])
var result string
for _, str := range strs[1:] {
if len(str) < n {
result = str
}
}
return result
}
解题思路:
- 初始公共前缀: 假定第一个字符串为公共前缀。
- 逐字符串更新公共前缀: 对数组中的每个字符串,逐字符比较,如果发现不匹配或者当前字符串长度小于公共前缀长度,就缩短公共前缀。
- 检查早期退出条件: 如果公共前缀在比较过程中变为空,直接返回空字符串,表示没有公共前缀。
- 最终返回: 如果所有字符串都检查完,返回最终的公共前缀。
func longestCommonPrefix(strs []string) string {
if len(strs) == 0 {
return ""
}
// 将第一个字符串设为初始的公共前缀
prefix := strs[0]
for _, str := range strs[1:] {
// 逐字符比较当前字符串和公共前缀
for len(str) < len(prefix) || (len(prefix) > 0 && str[:len(prefix)] != prefix) {
prefix = prefix[:len(prefix)-1]
}
// 如果公共前缀变为空,直接返回
if prefix == "" {
return ""
}
}
return prefix
}
1091. 二进制矩阵中的最短路径
题目:给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
路径途经的所有单元格的值都是 0 。 路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。 畅通路径的长度 是该路径途经的单元格总数。
解题思路:
- 从左上角开始,将起始位置加入到队列中,并标记为已访问。
- 从队列中依次取出位置,探索其周围八个方向的相邻位置,如果相邻位置可通过且未被访问,则将其加入队列,并标记为已访问,并将其路径长度加1。
- 不断重复这个过程,直到达到右下角位置或者队列为空。
- 如果成功到达右下角,则返回路径长度;否则返回-1表示无法到达。
type coordinate struct {
x, y int
}
func shortestPathBinaryMatrix(grid [][]int) int {
n := len(grid)
if n == 0 {
return -1
}
m := len(grid[0])
if grid[0][0] == 1 || grid[n-1][m-1] == 1 {
return -1
}
queue := list.List{}
queue.PushBack(coordinate{
x: 0,
y: 0,
})
var visitedMap = make(map[coordinate]bool)
visitedMap[coordinate{
x: 0,
y: 0,
}] = true
directions := [][]int{{0, -1}, {1, -1}, {1, 0}, {1, 1}, {0, 1}, {-1, 1}, {-1, 0}, {-1, -1}}
var steps = 1
for queue.Len() > 0 {
size := queue.Len()
for i := 0; i < size; i++ {
curr := queue.Remove(queue.Front()).(coordinate)
if curr.x == m-1 && curr.y == n-1 {
return steps
}
for _, dir := range directions {
next := coordinate{
x: curr.x + dir[0],
y: curr.y + dir[1],
}
// 有效&&未访问
if isValid(next, grid) && !visitedMap[next] {
queue.PushBack(next)
visitedMap[next] = true
}
}
}
steps++
}
return -1
}
func isValid(c coordinate, grid [][]int) bool {
n := len(grid)
return c.x >= 0 && c.x < n && c.y >= 0 && c.y < n && grid[c.x][c.y] == 0
}
2684. 矩阵中移动的最大次数
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid : 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。 返回你在矩阵中能够 移动 的 最大 次数。
示例 1:
输入:grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]] 输出:3 解释:可以从单元格 (0, 0) 开始并且按下面的路径移动:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。
示例 2:
输入:grid = [[3,2,4],[2,1,9],[1,1,7]] 输出:0 解释:从第一列的任一单元格开始都无法移动。
解题思路: @@@ dfs 解法
- 遍历每一行的第一个单元格,以该单元格为起点进行深度优先搜索。
- 在搜索过程中,递归地探索相邻单元格,并更新移动的最大次数。
- 使用一个二维数组 visited 来记录已经访问过的单元格,避免重复访问。
- 在搜索过程中,根据移动条件更新移动的最大次数 maxCount。
- 返回最大移动次数 maxCount 作为结果。
func maxMoves(grid [][]int) int {
m, n := len(grid), len(grid[0])
maxCount := 0
dirs := [][]int{{-1, 1}, {0, 1}, {1, 1}}
var dfs func(i, j int, visited [][]bool) int
dfs = func(i, j int, visited [][]bool) int {
if i < 0 || i >= m || j < 0 || j >= n || visited[i][j] {
return 0
}
visited[i][j] = true
count := j
for _, dir := range dirs {
newi, newj := i+dir[0], j+dir[1]
if newi >= 0 && newi < m && newj >= 0 && newj < n && grid[newi][newj] > grid[i][j] {
count = max(count, dfs(newi, newj, visited))
}
}
return count
}
for i := 0; i < m; i++ {
visited := make([][]bool, m)
for j := range visited {
visited[j] = make([]bool, n)
}
count := dfs(i, 0, visited)
maxCount = max(maxCount, count)
}
return maxCount
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
@@@
路径总和II
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func pathSum(root *TreeNode, targetSum int) [][]int {
var dfs func(node *TreeNode, sum int, path []int, result *[][]int)
dfs = func(node *TreeNode, sum int, path []int, result *[][]int) {
if node == nil {
return
}
// 添加当前节点的值到路径中
path = append(path, node.Val)
sum -= node.Val
// 检查是否到达叶子节点且路径和等于目标值
if sum == 0 && node.Left == nil && node.Right == nil {
// 复制当前路径以防止修改影响结果集
tmp := make([]int, len(path))
copy(tmp, path)
*result = append(*result, tmp)
}
// 继续递归遍历左子树和右子树
dfs(node.Left, sum, path, result)
dfs(node.Right, sum, path, result)
// 回溯:移除路径中的最后一个节点
path = path[:len(path)-1]
}
var result [][]int
dfs(root, targetSum, []int{}, &result)
return result
}
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
**示例 3: **
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示: 0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成
解题思路
滑动窗口法:
- 使用两个指针,一个指向窗口的起始位置,一个指向窗口的结束位置。
- 不断向右移动结束指针,并更新窗口中的字符集合,直到出现重复字符。
- 当出现重复字符时,移动起始指针,直到窗口中不再有重复字符。
- 在移动过程中更新最长子串的长度。
func lengthOfLongestSubstring(s string) int {
var mp = make(map[byte]int) // 存储字符及其索引
var startIdx int = 0 // 起始位置
var maxLen = 0
for endIdx, ch := range []byte(s) {
// 判断字符是否重复
if lastIdx, ok := mp[ch]; ok && lastIdx >= startIdx {
startIdx = lastIdx + 1 // 更新起始位置
}
mp[ch] = endIdx // 更新字符的最近出现位置
currLen := endIdx-startIdx+1
if currLen > maxLen {
maxLen = currLen
}
}
return maxLen
}
105.根据前序和中序构建二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7] 示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
解题思路:
- 前序:root-left-right 中序:left-root-right 后序:left-right-root
- 找到根节点
- 根据根节点在中序遍历中,左边为左子树,右边为右子树
- 递归构造子树
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func buildTree(preorder []int, inorder []int) *TreeNode {
var root *TreeNode
if len(preorder) == 0 || len(inorder) == 0 {
return nil
}
ans := preorder[0]
root = &TreeNode{Val: ans}
var idx int
for i, v := range inorder {
if v == ans {
idx = i
break
}
}
// 左开右闭
root.Left = buildTree(preorder[1:1+idx], inorder[:idx])
root.Right = buildTree(preorder[1+idx:], inorder[idx+1:])
return root
}
0129.求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。 叶节点 是指没有子节点的节点。
示例 1: 输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此,数字总和 = 12 + 13 = 25
示例 2: 输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026
提示: 树中节点的数目在范围 [1, 1000] 内 0 <= Node.val <= 9 树的深度不超过 10
解题思路
- 使用深度优先递归。
- 在每个节点,将当前节点的值乘以 10 并将其添加到路径和中。
- 如果当前节点是叶节点,则将路径和添加到总和中。
- 继续递归遍历左子树和右子树,更新路径和
func sumNumbers(root *TreeNode) int {
var dfs func(root *TreeNode, pathSum int) int
dfs = func(root *TreeNode, pathSum int) int {
if root == nil {
return 0
}
pathSum = pathSum * 10 + root.Val
if root.Left == nil && root.Right == nil {
return pathSum
}
return dfs(root.Left, pathSum) + dfs(root.Right, pathSum)
}
return dfs(root, 0)
}
二叉树最大深度
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1: 输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2: 输入:root = [1,null,2] 输出:2
提示: 树中节点的数量在 [0, 10⁴] 区间内。 -100 <= Node.val <= 100
解题思路
- 使用深度优先搜索(DFS)遍历二叉树。
- 在每个结点,计算其左右子树的最大深度,并返回两者中较大的值加上 1
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
leftDepth := maxDepth(root.Left)
rightDepth := maxDepth(root.Right)
return max(rightDepth, leftDepth) + 1
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1: 输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2: 输入:root = [1,2,2,null,3,null,3] 输出:false
提示: 树中节点数目在范围 [1, 1000] 内 -100 <= Node.val <= 100
解题思路
- 递归法(dfs)
- 终止条件是左右节点都是nil
- 迭代法(bfs)
func isSymmetric(root *TreeNode) bool {
if root == nil {
return false
}
var queue = make([]*TreeNode, 0)
queue = append(queue, root.Left, root.Right)
for len(queue) > 0 {
left, right := queue[0], queue[1]
queue = queue[2:]
if left == nil && right == nil {
continue
}
if left == nil || right == nil || left.Val != right.Val {
return false
}
// 注意:添加子树时顺序,由于对称性问题
queue = append(queue, left.Left, right.Right)
queue = append(queue, left.Right, right.Left)
}
return true
}
func isSymmetric1(root *TreeNode) bool {
if root == nil {
return true
}
return isMirror(root.Left, root.Right)
}
func isMirror(left, right *TreeNode) bool {
if left == nil && right == nil {
return true
}
if left == nil || right == nil || left.Val != right.Val {
return false
}
return isMirror(left.Left, right.Right) && isMirror(left.Right, right.Left)
}
110.平衡二叉树
给定一个二叉树,判断它是否是 平衡二叉树
示例 1: 输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2: 输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3: 输入:root = [] 输出:true
提示: 树中的节点数在范围 [0, 5000] 内 -10⁴ <= Node.val <= 10⁴
解题思路:
递归法:
- 首先,编写一个函数来计算树的高度。
- 然后,递归地检查每个节点是否平衡,即判断左右子树的高度差是否小于等于1,并且左右子树也都是平衡的。
- 最后,如果树是平衡的,则返回True,否则返回False。
func isBalanced(root *TreeNode) bool {
if root == nil {
return true
}
leftHeight := getHeight(root.Left)
rightHeight := getHeight(root.Right)
if math.Abs(float64(leftHeight-rightHeight)) > 1 {
return false
}
return isBalanced(root.Left) && isBalanced(root.Right)
}
func getHeight(node *TreeNode) int {
if node == nil {
return 0
}
leftHeight := getHeight(node.Left)
rightHeight := getHeight(node.Right)
return int(math.Max(float64(leftHeight), float64(rightHeight)))+1 节点自身高度
}
Level Order Traversal (102. Binary Tree Level Order Traversal)
Given a binary tree, return the level order traversal of its nodes' values.
Example:
Input:
3
/ \
9 20
/ \
15 7
Output:
[
[3],
[9,20],
[15,7]
]
Constraints:
- The number of nodes in the tree is in the range [0, 2000].
- -1000 <= Node.val <= 1000
Approach: We can solve this problem using a breadth-first search (BFS) approach. We'll use a queue to store nodes at each level and process them level by level.
Algorithm:
- Create an empty result list res to store the level order traversal.
- Create a queue q and enqueue the root node.
- While the queue is not empty:
- a. Dequeue all nodes at the current level and store their values in a temporary list level.
- b. Add level to the result list res.
- c. Enqueue all children of the nodes at the current level.
- Return the result list res.
Code:
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func levelOrder(root *TreeNode) [][]int {
if root == nil {
return [][]int{}
}
var result [][]int
var queue = []*TreeNode{root}
for len(queue) > 0 {
size := len(queue)
var level []int
for i := 0; i < size; i++ {
node := queue[i]
level = append(level, node.Val)
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
queue = queue[size:]
result = append(result, level)
}
return result
}
543.二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1: 输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2: 输入:root = [1,2] 输出:1
提示: 树中节点数目在范围 [1, 10⁴] 内 -100 <= Node.val <= 100
解题思路
- 定义DFS函数: 该函数接受一个节点作为参数,返回该节点为根的子树的最大深度,并同时更新全局变量 maxDiameter 来记录目前为止找到的最大直径。
- 递归计算子树深度: 对于每个节点,递归计算其左子树和右子树的最大深度 leftDepth 和 rightDepth。
- 更新直径: 当前节点的左右子树深度之和 leftDepth + rightDepth 表示经过该节点的最长路径的长度,将其与 maxDiameter 比较并更新 maxDiameter。
- 返回最大深度: 函数返回 1 + max(leftDepth, rightDepth),表示以当前节点为根的子树的最大深度。
func diameterOfBinaryTree(root *TreeNode) int {
var maxDiameter int
var dfs func(node *TreeNode) int
dfs = func(node *TreeNode) int {
if node == nil {
return 0
}
leftDepth := dfs(node.Left)
rightDepth := dfs(node.Right)
if leftDepth + rightDepth > maxDiameter {
maxDiameter = leftDepth + rightDepth
}
return 1 + max(leftDepth, rightDepth)
}
dfs(root)
return maxDiameter
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
验证二叉搜索树
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node’s key. The right subtree of a node contains only nodes with keys greater than the node’s key. Both the left and right subtrees must also be binary search trees. Example 1:
2
/ \
1 3
Input: [2,1,3] Output: true Example 2:
5
/ \
1 4
/ \
3 6
Input: [5,1,4,null,null,3,6] Output: false Explanation: The root node's value is 5 but its right child's value is 4.
题目大意 给定一个二叉树,判断其是否是一个有效的二叉搜索树。假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
解题思路
- 递归法
- 检查每个节点,左节点是否小于根节点,右节点大于根节点
- 中序遍历法
- 正确的二叉搜索树,按中序遍历,是按左、中、右顺序从小到大排序,如果出现逆序则不是正确的二叉搜索树
func isValidBST(root *TreeNode) bool {
return Helper(root, math.MinInt32, math.MaxInt32)
}
func Helper(root *TreeNode, min, max int) bool {
if root == nil {
return true
}
if root.Val < min || root.Val > max {
return false
}
return Helper(root.Left, min, root.Val-1) && Helper(root.Right, root.Val+1, max)
}
144.二叉树进行前序遍历
递归法:递归方法比较直接,直接按照前序遍历的定义进行递归调用, 根-左-右
func preorderTraversal(root *TreeNode) []int {
var result []int
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
result = append(result, node.Val)
dfs(node.Left)
dfs(node.Right)
}
dfs(root)
return result
}
迭代法:
- 初始化一个栈,将根节点压入栈中。
- 当栈不为空时,弹出栈顶节点,访问该节点。
- 将右子节点压入栈(如果存在),然后将左子节点压入栈(如果存在)。
注意:压栈的顺序是先右后左,这样出栈时才能先左后右,符合前序遍历的顺序。
func preorderTraversal1(root *TreeNode) []int {
if root == nil {
return nil
}
var result []int
var stack = []*TreeNode{root}
for len(stack) > 0 {
node := stack[len(stack)-1]
// 更新stack
stack = stack[:len(stack)-1]
result = append(result, node.Val)
if node.Right != nil {
stack = append(stack, node.Right)
}
if node.Left != nil {
stack = append(stack, node.Left)
}
}
return result
}
0155.最小栈
设计一个支持 push,pop, top 操作,并能在常数时间内检索到最小元素的栈。
- push(x) -- 将元素 x 推入栈中
- pop() -- 删除栈顶的元素
- top() -- 获取栈顶元素
- getMin() -- 检索栈中最小元素
type MinStack struct {
stack []int
minStack []int
}
/** initialize your data structure here. */
func Constructor() MinStack {
return MinStack{
stack: make([]int, 0),
minStack: make([]int, 0),
}
}
func (this *MinStack) Push(x int) {
this.stack = append(this.stack, x)
// 注意边界条件 <= 和 minStack 为空时
if len(this.minStack) == 0 || x <= this.minStack[len(this.minStack)-1] {
this.minStack = append(this.minStack, x)
}
}
func (this *MinStack) Pop() {
if len(this.stack) == 0 {
return
}
if x := this.stack[len(this.stack)-1]; x == this.minStack[len(this.minStack)-1] {
this.minStack = this.minStack[:len(this.minStack)-1]
}
this.stack = this.stack[:len(this.stack)-1]
}
func (this *MinStack) Top() int {
if len(this.stack) == 0 {
return 0
}
return this.stack[len(this.stack)-1]
}
func (this *MinStack) GetMin() int {
if len(this.minStack) == 0 {
return 0
}
return this.minStack[len(this.minStack)-1]
}
有效括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()" 输出:true
示例 2:
输入:s = "()[]{}" 输出:true
示例 3:
输入:s = "(]" 输出:false
提示:
1 <= s.length <= 10⁴ s 仅由括号 '()[]{}' 组成
解题思路
这道题可以用栈来解决。遍历字符串,遇到左括号就入栈,遇到右括号就判断栈顶元素是否与之匹配,匹配则弹出栈顶元素,否则返回False。最后如果栈为空,则说明所有括号都匹配成功,返回True,否则返回False。
func isValid(s string) bool {
if s == "" {
return true
}
var mp = map[byte]byte{'{':'}', '[':']', '(':')'}
var stack []byte
for i := 0; i < len(s); i++ {
if s[i] == '{' || s[i] == '(' || s[i] == '[' {
// 入栈
stack = append(stack, s[i])
}else {
if len(stack) == 0 || mp[stack[len(stack)-1]] != s[i] {
return false
}
// 出栈
stack = stack[:len(stack)-1]
}
}
return len(stack)==0
}
394.字符串编码
解题思路:
- 解析数字,注意:多位数字情况,例如:123[ab]
- 累计字符串
func decodeString(s string) string {
var currNum = 0 // [ 前的计数
var currStr string // 当前已完成编码的字符串
var stack []string // 数字+[]内的字符串
for _, ch := range s {
// 处理数字
if ch >= '0' && ch <= '9' {
tmpNum, _ := strconv.Atoi(string(ch))
// 兼容多位数字
currNum = currNum * 10 + tmpNum
}else if ch == '[' { // 重复字符串开始
stack = append(stack, currStr)
stack = append(stack, strconv.Itoa(currNum))
// 重置 currNum, currStr
currNum = 0
currStr = ""
}else if ch == ']' { // 重复字符串结束
// 弹出重复次数
repeatNum, _ := strconv.Atoi(stack[len(stack)-1])
stack := stack[:len(stack)-1] // 更新stack
// 弹出前面已编码的字符串
prevStr := stack[len(stack)-1]
stack := stack[:len(stack)-1] // 再更新stack
// 拼接已编码的字符串
currStr = prevStr + strings.Repeat(currStr, repeatNum)
}else {
currStr += string(ch)
}
}
return currStr
}
字符串消消乐
给定一个由数字组成的字符串,要求你按照以下规则消除相邻的数字,并计算最终剩下的字符串长度:
• 当字符串中相邻的两个数字相加等于 10 时,这两个数字会被消除,剩下的部分会拼接成新的字符串,继续按照相同的规则消除。 • 每次消除只发生在相邻的数字之间,并且每次只会消除一对相邻数字。 • 你需要计算最终剩下的字符串长度,使得字符串无法再消除时的长度最小。
解题思路:
- 用栈方法
- 将字符串转为数字, 与'0'减法运算
- 遍历,每逢当前元素和栈顶元素和为10,执行出栈(消除),否则入栈
- 最终返回栈的长度
func minLengthAfterElimination(s string) int {
stack := []int{}
// 遍历字符串中的每个字符
for i := 0; i < len(s); i++ {
num := int(s[i] - '0') // 将字符转换为数字
// 如果栈不为空且栈顶元素与当前元素之和为10,执行消除操作
if len(stack) > 0 && stack[len(stack)-1]+num == 10 {
// 消除栈顶元素
stack = stack[:len(stack)-1]
} else {
// 否则将当前元素压入栈中
stack = append(stack, num)
}
}
// 返回栈的长度即为最终剩余字符串长度
return len(stack)
}
贪心
模板代码
// 贪心算法函数
func greedyAlgorithm(items []int, condition func(int) bool, selectItem func([]int) int) int {
// 初始化
result := 0
// 排序
sort.Slice(items, func(i, j int) bool {
// 根据具体问题定义排序规则
return items[i] < items[j]
})
// 贪心选择
for _, item := range items {
if condition(item) {
// 做出选择
result += selectItem(item)
// 更新状态
// 在一些问题中,你可能需要更新数据或状态
}
}
return result
}
经典题目
- 分发饼干/糖果(135,455)
- 根据身高重建队列(406)
- 买卖股票最佳时机(122,714)
- 跳跃游戏(45,55)
- 最大子序和(53)
- 区间问题(56,763)
5.Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s.
Example:
Input: s = "babad"
Output: "bab"
Algorithm:
- Initialize a 2D array dp of size m x n, where m is the length of the input string s and n is the maximum length of a palindromic substring.
- Iterate through the input string s and for each character c, check if it is the same as the previous character c-1. If it is, mark the corresponding cell in dp as true.
- Iterate through the input string s and for each character c, check if it is the same as the next character c+1. If it is, mark the corresponding cell in dp as true.
- Iterate through the 2D array dp and find the longest palindromic substring.
Code:
// 动态规划
func longestPalindrome(s string) string {
// 长度为1 肯定是回文串
if len(s) <= 1 {
return s
}
// start 代表回文串开始下标,end 代表结束下标
var start, maxLen, length = 0, 1, len(s)
// 二维数组dp[i][j] 表示索引 i 到索引 j 是否回文,true 是,否则不是
var dp = make([][]bool, len(s))
// 长度为 1 的肯定是回文, 所有的 dp[i][i] 都是 true
for i := 0; i < length; i++ {
// 初始化数组
dp[i] = make([]bool, length)
dp[i][i] = true
}
// i,j 是回文左右下标,k 是中间回文子串长度
// 回文判断规则:s[i]=s[j] 其中 j = i+中间回文子串长度,由于从0开始遍历,下标需要减1
// 边界情况:
// k长度为2,中间子串长度0也是回文
// 中间子串下标规则 dp[i+1][j-1]
// 由于 k 长度 1 都是回文,从长度 2 开始遍历
for k := 2; k <= length; k++ {
for i := 0; i <= length-k; i++ {
j := i + k - 1
if s[i] == s[j] && (k == 2 || dp[i+1][j-1]) {
dp[i][j] = true
// 更新回文子串长度
if k > maxLen {
start = i
maxLen = k
}
}
}
}
return s[start : start+maxLen]
}
中心扩展法
// 中心扩展
func longestPalindrome1(s string) string {
if len(s) < 2 {
return s
}
// 起始位置、结束位置
start, end := 0, 0
for i := 0; i < len(s); i++ {
// 以一个字符中心扩展
exp1 := expand(s, i, i)
// 以两个字符中心扩展
exp2 := expand(s, i, i+1)
maxLen := max(exp1, exp2)
// 在每次扩展后,我们比较当前回文串的长度和已知的最长回文子串长度,
// 如果大于最长回文子串长度,则更新最长回文子串的起始位置和结束位置。
if maxLen > end-start+1 {
// 起始位置=当前位置i - (maxLen-1)/2
start = i - (maxLen-1)/2
// 结束位置=当前位置i + maxLen/2
end = i + maxLen/2
}
}
return s[start : end+1]
}
func expand(s string, left, right int) int {
for left >= 0 && right < len(s) && s[left] == s[right] {
left--
right++
}
// 因为扩展时左右边界都多扩展了一步
return right - left - 1
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
64.最小路径和
解题思路
- 动态规划,创建一个二维数组dp[i][j],代表(0,0) 到 (i,j) 的最小路径和
- dp 初始化,首行首列遍历填充
- 状态转移方程 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + matrix[i][j], 即(i,j)左边,上边的最小值 + 自身
代码实现
func minPathSum(grid [][]int) int {
if len(grid) == 0 || len(grid[0]) == 0 {
return 0
}
m, n := len(grid), len(grid[0])
dp := make([][]int, m)
for i := range dp {
dp[i] = make([]int, n)
}
dp[0][0] = grid[0][0]
for i := 1; i < m; i++ {
dp[i][0] = dp[i-1][0] + grid[i][0]
}
for j := 1; j < n; j++ {
dp[0][j] = dp[0][j-1] + grid[0][j]
}
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
dp[i][j] = int(math.Min(float64(dp[i-1][j]), float64(dp[i][j-1]))) + grid[i][j]
}
}
return dp[m-1][n-1]
}
74. 搜索二维矩阵
题目:给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例1:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true 示例2:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
解题思路
- 二分法: 二分查找行、二分查找列。注意点,查找行时,如果等于某行第一个元素,找到目标 如果大于某行第一个元素,继续往下寻找 如果小雨某行第一个元素,停止搜索,并且往上一行寻找 所以 最终right 就是该目标所在的行索引。
- 利用从左到右,从上到下递增的矩阵特性,从右上角开始搜索,小于往左找,大于往下找
解法一
func searchMatrix(matrix [][]int, target int) bool {
m := len(matrix)
if m == 0 {
return false
}
n := len(matrix[0])
if n == 0 {
return false
}
// 行二分
var left, right = 0, m - 1
for left <= right {
mid := (left + right) / 2
if target > matrix[mid][0] {
left = mid + 1
} else if target < matrix[mid][0] {
right = mid - 1
} else {
return true
}
}
// 如果等于某行第一个元素,找到目标
// 如果大于某行第一个元素,继续往下寻找
// 如果小雨某行第一个元素,停止搜索,并且往上一行寻找
// 所以 最终right 就是该目标所在的行索引
if right < 0 {
return false
}
row := right
// 二分查找列
l, r := 0, n-1
for l <= r {
mid := (l + r) / 2
if target > matrix[row][mid] {
l = mid + 1
} else if target < matrix[row][mid] {
r = mid - 1
} else {
return true
}
}
return false
}
解法二
func searchMatrix1(matrix [][]int, target int) bool {
m := len(matrix)
if m == 0 {
return false
}
n := len(matrix[0])
if n == 0 {
return false
}
var row, col = 0, n - 1
for col >= 0 && row < m {
if matrix[row][col] == target {
return true
} else if matrix[row][col] > target {
col--
} else {
row++
}
}
return false
}
搜索二维矩阵II
解题思路:
- 从右上角开始查
- 行列双指针
func searchMatrix(matrix [][]int, target int) bool {
if len(matrix) == 0 || len(matrix[0]) == 0 {
return false
}
m := len(matrix)
n := len(matrix[0])
i,j := 0, n-1
for i < m && j >= 0 {
if matrix[i][j] > target {
j--
}else if matrix[i][j] < target {
i++
}else {
return true
}
}
return false
}
162.寻找峰值
解题思路:
- 选择数组的中间元素nums[mid]。
- 如果nums[mid]大于其左侧元素nums[mid - 1]和右侧元素nums[mid + 1](如果存在),则nums[mid]就是一个峰值元素。
- 如果nums[mid]小于nums[mid + 1],说明峰值一定存在右侧,因为元素从mid往mid+1处上升。
- 如果nums[mid]小于nums[mid - 1],说明峰值一定存在左侧。
func findPeakElement(nums []int) int {
n := len(nums)
left, right := 0, n-1
for left < right {
mid := left + (right-left)/2
if nums[mid] > nums[mid+1] {
right = mid
}else {
left = mid+1
}
}
return left
}
7.整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2³¹, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123 输出:321
示例 2:
输入:x = -123 输出:-321
示例 3:
输入:x = 120 输出:21
示例 4:
输入:x = 0 输出:0
提示:
-2³¹ <= x <= 2³¹ - 1
Related Topics 数学 👍 3983 👎 0
func reverse(x int) int {
var result = 0
for x != 0 {
result = result*10 + x%10
x /= 10
if result > math.MaxInt32 || result < math.MinInt32 {
return 0
}
}
return result
}
9.回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121 输出:true
示例 2:
输入:x = -121 输出:false 解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10 输出:false 解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
-2³¹ <= x <= 2³¹ - 1
进阶:你能不将整数转为字符串来解决这个问题吗?
Related Topics 数学 👍 2837 👎 0
func isPalindrome(x int) bool {
if x < 0 {
return false
}
ans := fmt.Sprint(x)
var reversed string
for i := len(ans) - 1; i >= 0; i-- {
reversed += string(ans[i])
}
if ans == reversed {
return true
}
return false
}
func isPalindrome1(x int) bool {
if x < 0 {
return false
}
// 边界问题1
// 如果最后一位是0,除了0本身也不是回文
if x != 0 && x%10 == 0 {
return false
}
var reversed int
for x > reversed {
reversed = reversed*10 + x%10
x /= 10
}
// 边界问题2
// 如果x长度是奇数,12321 循环结束后 x = 12 reversed = 123 也是回文数
return x == reversed || x == reversed/10
}
470. rand7实现rand10
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数。请注意,这不是传递给 rand10() 的参数。
示例 1: 输入: 1 输出: [2]
示例 2: 输入: 2 输出: [2,8]
示例 3: 输入: 3 输出: [3,8,10]
提示: 1 <= n <= 10⁵
进阶: rand7()调用次数的 期望值 是多少 ? 你能否尽量少调用 rand7() ?
解题思路
- 首先,调用两次 rand7(),分别得到两个随机数 a 和 b。
- 将这两个随机数转换成一个二维坐标 (a, b),这个坐标落在一个 7x7 的网格中。
- 将这个 7x7 的网格映射到一个 10x10 的网格中,并将超出 10x10 网格的部分舍弃。
- 如果映射后的坐标落在 10x10 网格内,则将其转换为 [1,10] 范围内的随机数。
- 否则,重复步骤 1-4,直到生成一个有效的随机数。
func rand10() int {
for {
a, b := rand7(), rand7()
index := (a-1)*7 + b
if index <= 40 {
return index%10 + 1
}
}
}
LRU Cache (146. LRU Cache)
Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.
get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.
Example:
LRUCache cache = new LRUCache( 2 /* capacity */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // returns 1
cache.put(3, 3); // evicts key 2
cache.get(2); // returns -1 (not found)
cache.put(4, 4); // evicts key 1
cache.get(1); // returns -1 (not found)
cache.get(3); // returns 3
cache.get(4); // returns 4
Constraints:
- 1 <= capacity <= 1000
- 0 <= key <= 1000
- 0 <= value <= 1000
- At most 10000 calls will be made to get and put.
Approach:
We can solve this problem using a combination of a hash map and a doubly linked list. The hash map will store the keys and their corresponding nodes in the linked list, and the linked list will maintain the order of the nodes based on their recent usage.
Algorithm:
- Create a hash map cache to store the keys and their corresponding nodes in the linked list.
- Create a doubly linked list dll to store the nodes in the order of their recent usage.
- Implement the get operation:
- Check if the key exists in the cache. If it does, move the corresponding node to the front of the linked list and return the value.
- If the key does not exist, return -1.
- Implement the put operation:
- If the key already exists in the cache, update the value and move the corresponding node to the front of the linked list.
- If the key does not exist and the cache is full, remove the least recently used node (the node at the end of the linked list) and add the new node to the front of the linked list.
- If the key does not exist and the cache is not full, add the new node to the front of the linked list.
代码实现:
type LRUCache struct {
Cap int
Keys map[int]*list.Element // map 保存双向链表的结点
Lists *list.List
}
type kv struct {
K, V int
}
func Constructor(capacity int) LRUCache {
return LRUCache{
Cap: capacity,
Keys: make(map[int]*list.Element),
Lists: &list.List{},
}
}
// LRUCache 的 Get 操作很简单,在 map 中直接读取双向链表的结点。如果 map 中存在,将它移动到双向链表的表头,并返回它的 value 值,如果 map 中不存在,返回 -1。
func (this *LRUCache) Get(key int) int {
if element, ok := this.Keys[key]; ok {
this.Lists.MoveToFront(element)
return element.Value.(kv).V
}
return -1
}
// 先查询 map 中是否存在 key,如果存在,更新它的 value,并且把该结点移到双向链表的表头。
// 如果 map 中不存在,新建这个结点加入到双向链表和 map 中。
// 最后别忘记还需要维护双向链表的 cap,如果超过 cap,需要淘汰最后一个结点,双向链表中删除这个结点,map 中删掉这个结点对应的 key。
func (this *LRUCache) Put(key int, value int) {
if el, ok := this.Keys[key]; ok {
el.Value = kv{
K: key,
V: value,
}
this.Lists.MoveToFront(el)
} else {
el := this.Lists.PushFront(kv{
K: key,
V: value,
})
this.Keys[key] = el
}
if this.Lists.Len() > this.Cap {
el := this.Lists.Back()
this.Lists.Remove(el)
delete(this.Keys, el.Value.(kv).K)
}
}
https://learn.lianglianglee.com/文章/领域驱动设计在互联网业务开发中的实践.md
系统设计
系统设计
- 服务器扩展
- 数据库选型
- 数据库扩展
- 负载均衡器
- 数据库复制
- 缓存
- CDN
- 数据中心
- 消息队列
- 日志记录、指标采集、监控告警
Gin 框架源码阅读
项目结构
- gin.go:了解引擎初始化和主入口。
- routergroup.go:理解路由的定义和注册。
- tree.go:深入研究路由匹配的具体实现。
- context.go:理解请求的处理过程。
- middleware.go:学习中间件机制。
gin 拦截器实现原理
在 Gin 框架中,中间件的实现主要依赖于 RouterGroup 和 Engine 结构体中的 HandlersChain 类型。HandlersChain 是一个处理函数链,每个函数都会在请求处理过程中被调用。 HandlersChain: 这是一个 HandlerFunc 的切片,表示一系列中间件函数。
func (group *RouterGroup) Use(handlers ...HandlerFunc) IRoutes {
group.Handlers = append(group.Handlers, handlers...)
return group.returnObj()
}
拦截器执行过程:
- 初始化中间件链
handlers := append(group.Handlers, specificHandlers...)
- 中间件的调用
for _, handler := range handlers {
handler(c)
}
- 请求处理与响应 最终的处理函数是中间件链的最后一个函数,它负责生成响应并将其返回给客户端。 中间件之间的控制流: 中间件函数可以调用 c.Next() 来继续执行下一个中间件,也可以调用 c.Abort() 来停止后续中间件的执行并直接返回响应。
func someMiddleware(c *Context) {
// 中间件逻辑
c.Next() // 继续执行下一个中间件
}
func anotherMiddleware(c *Context) {
// 中间件逻辑
c.Abort() // 停止后续中间件执行
}
Gin 路由实现原理
Gin 框架的路由实现主要依赖于一种高效的数据结构——前缀树(Trie),以及一系列的算法和结构体来管理和匹配路由。
路由数据结构
- Engine: 复杂负责管理所有的路由和中间件。
- trees: 一个映射,键是 HTTP 方法(如 “GET”, “POST”),值是对应的方法路由树(node 类型)。
type Engine struct {
RouterGroup
trees map[string]*node // 记录不同 HTTP 方法的路由树
}
node 结构
type node struct {
path string // 节点的路径部分。
children []*node // 子节点
handlers HandlersChain // 处理函数链
maxParams uint16
isWild bool
}
路由注册 addRoute 方法将路由路径和处理函数链添加到路由树中。
func (e *Engine) addRoute(method, path string, handlers HandlersChain) {
root := e.trees[method]
if root == nil {
root = new(node)
e.trees[method] = root
}
root.addRoute(path, handlers)
}
路由匹配 findRoute 方法用于根据请求路径在路由树中查找匹配的路由。
func (n *node) findRoute(path string) (*node, map[string]string) {
params := make(map[string]string)
current := n
// 遍历节点,逐个字符匹配路径
for {
if len(path) == 0 {
if current.handlers != nil {
return current, params
}
return nil, nil
}
c := path[0]
path = path[1:]
child, _ := current.matchChild(c)
if child == nil {
return nil, nil
}
// 如果节点包含路径参数,则提取参数并存储在 params 字典中。
if child.isWild {
paramName := child.path[1:]
params[paramName] = extractParam(path, child.path)
path = path[len(child.path)-1:]
}
current = child
}
}
Docker
Docker 隔离技术
cgroups(控制组)
cgroups 是 Linux 内核提供的一种机制,用于限制、记录和隔离进程组的资源(CPU、内存、磁盘 I/O 等)。通过 cgroups,Docker 可以控制容器使用的 CPU 资源。具体来说,Docker 使用以下两种 CPU 子系统来实现 CPU 隔离:
- cpu.shares:相对权重控制,表示相对 CPU 使用权重。默认值是 1024,值越大,分配的 CPU 时间就越多。它用于不同容器之间的 CPU 时间片的相对分配。
- cpu.cfs_quota_us 和 cpu.cfs_period_us:绝对限制控制。CFS(完全公平调度器)周期和配额设置。通过这两个参数,可以设置容器在一个周期内可以使用的 CPU 时间。比如,设置 cpu.cfs_period_us 为 100000 (100 ms),cpu.cfs_quota_us 为 20000 (20 ms),表示这个容器在每 100 ms 内最多只能使用 20 ms 的 CPU 时间。
配置方法:
# 表示容器最多可以使用 50% 的 CPU 资源
docker run -it --cpus=".5" ubuntu /bin/bash
查看限制配置:
cat /sys/fs/cgroup/cpu/docker/<container_id>/cpu.cfs_period_us
cat /sys/fs/cgroup/cpu/docker/<container_id>/cpu.cfs_quota_us
其他CPU隔离方式:
- CPU共享(CPU Shares): 通过--cpu-shares参数设置容器的CPU权重。
- CPU亲和性(CPU Affinity): 使用--cpuset-cpus参数将容器绑定到特定CPU核心。
命名空间(namespaces)
命名空间提供了进程间的隔离。Docker 使用以下几种命名空间:
- PID 命名空间:隔离进程 ID。
- NET 命名空间:隔离网络接口、IP 地址、防火墙规则等。
- IPC 命名空间:隔离进程间通信机制。
- MNT 命名空间:隔离挂载点。
- UTS 命名空间:隔离主机名和域名。
- User 命名空间:隔离用户和用户组。